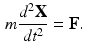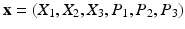Springer International Publishing Switzerland 2015
Thomas Witelski and Mark Bowen Methods of Mathematical Modelling Springer Undergraduate Mathematics Series 10.1007/978-3-319-23042-9_1
1. Rate Equations
Many real-world systems can be described in terms of the evolution of state variables for various system properties, starting from given initial configurations. The simplest models for such problems are given by ordinary differential equations (ODE) describing the rates of change of the state variables as functions of time.
Applications include:
Mechanics : motion of masses subjected to forces
Modern physics : radioactive decay of materials
Statistical systems : queues, games, multi-stage processes
Chemistry/Biochemistry : chemical reactions
Biology : epidemic models for diseases in populations
Ecology : dynamics of populations of predator and prey species
While the dynamics in some of these applications may rest on discrete events, like the radioactive decay of an atom or the death of an individual in a population, when averaged over large populations, reliable mean-rates of activities can occur; this is the basis for writing ODE rate equations and other continuous models . ODEs cannot describe all of the details of the processes occurring in these systems, but they provide a good starting point for investigations, often yielding accurate predictions of various phenomena.
For a system involving n evolving properties, the governing mathematical problem is typically written in the form
where the vector of state variables,
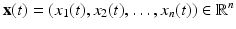
, describes n properties of interest in the system, evolving for times
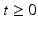
and starting from a given initial state
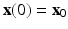
. The rate functions for the rates of change of each
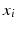
,
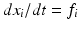
, have similarly been collected in a vector,
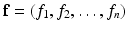
, where each
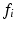
can potentially depend on all of the state variables.
System (), where the rate functions have an explicit dependence on time, is called non-autonomous . In such systems, the solutions depend on the particular details of externally imposed time-dependent influences. In this chapter, we will focus on autonomous systems ,
where the rates only depend on the current state of the solution. These systems describe natural or unforced behaviour innate to the system and are the traditional starting points for studying new classes of problems. In later chapters we will return to the influence of inhomogeneous forcing with applications such as control theory and driven systems.
Problems that can be stated in the form () are called dynamical systems , where the independent variable t usually represents time, but may also represent other properties depending on the context of the system. The most fundamental issues to be addressed for a given dynamical system are
Dynamics : What is the behaviour of the solution for
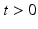
starting from given initial conditions
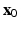
? (i.e. Will the solution be oscillatory, or monotone increasing, or exponentially decaying? Do solutions of certain types exist for any
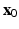
? Does a unique solution exist?....)
Stability : Can the systems behaviour be predicted starting from broad sets of initial conditions? (i.e. Do the solutions starting from other initial conditions follow the behaviour of the solution starting from
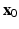
?)
In the simplest cases (in dimensions
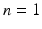
and
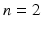
), the complete behaviour of systems can be understood from local properties of the rate functions and geometric descriptions of the set of solutions. This can yield a complete characterisation of the dynamics without the need to attempt to explicitly construct the solutions. For
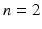
, this geometric approach is called phase plane analysis and forms the basis of (general) dynamical systems theory .
1.1 The Motion of Particles
A classic example of a dynamical system from mechanics is the system for motion of a particle, where the unknowns describing the state of the particle are its position,
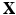
, and momentum,
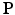
. The rate of change of position is the velocity, and from Newtons second law [67, 91], the rate of change of momentum is given by the net applied force,
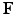
, so we can write
where
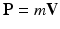
and the applied forces could depend on position and momentum. If the mass is constant, then these equations can be combined to give the familiar law of motion linking mass times acceleration to the net applied force,
Note that every n th order autonomous differential equation can always be re-expressed in the form of a system of n (first-order) rate equations. Defining
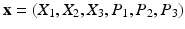












![Thomas Mailund [Thomas Mailund] - Beginning Data Science in R: Data Analysis, Visualization, and Modelling for the Data Scientist](/uploads/posts/book/119629/thumbs/thomas-mailund-thomas-mailund-beginning-data.jpg)

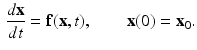
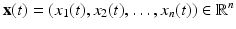 , describes n properties of interest in the system, evolving for times
, describes n properties of interest in the system, evolving for times 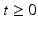 and starting from a given initial state
and starting from a given initial state 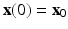 . The rate functions for the rates of change of each
. The rate functions for the rates of change of each 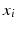 ,
, 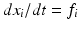 , have similarly been collected in a vector,
, have similarly been collected in a vector, 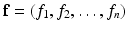 , where each
, where each 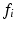 can potentially depend on all of the state variables.
can potentially depend on all of the state variables.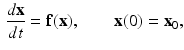
 starting from given initial conditions
starting from given initial conditions 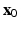 ? (i.e. Will the solution be oscillatory, or monotone increasing, or exponentially decaying? Do solutions of certain types exist for any
? (i.e. Will the solution be oscillatory, or monotone increasing, or exponentially decaying? Do solutions of certain types exist for any 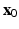 ? Does a unique solution exist?....)
? Does a unique solution exist?....)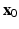 ?)
?)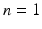 and
and 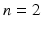 ), the complete behaviour of systems can be understood from local properties of the rate functions and geometric descriptions of the set of solutions. This can yield a complete characterisation of the dynamics without the need to attempt to explicitly construct the solutions. For
), the complete behaviour of systems can be understood from local properties of the rate functions and geometric descriptions of the set of solutions. This can yield a complete characterisation of the dynamics without the need to attempt to explicitly construct the solutions. For 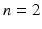 , this geometric approach is called phase plane analysis and forms the basis of (general) dynamical systems theory .
, this geometric approach is called phase plane analysis and forms the basis of (general) dynamical systems theory .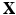 , and momentum,
, and momentum, 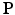 . The rate of change of position is the velocity, and from Newtons second law [67, 91], the rate of change of momentum is given by the net applied force,
. The rate of change of position is the velocity, and from Newtons second law [67, 91], the rate of change of momentum is given by the net applied force, 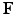 , so we can write
, so we can write 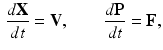
 and the applied forces could depend on position and momentum. If the mass is constant, then these equations can be combined to give the familiar law of motion linking mass times acceleration to the net applied force,
and the applied forces could depend on position and momentum. If the mass is constant, then these equations can be combined to give the familiar law of motion linking mass times acceleration to the net applied force,