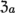Multi-Body Kinematics and Dynamics with Lie Groups
Dominique P. Chevallier
Jean Lerbet
Series Editor
Nol Challamel


Copyright
First published 2018 in Great Britain and the United States by ISTE Press Ltd and Elsevier Ltd
Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address:
ISTE Press Ltd
27-37 St Georges Road
London SW19 4EU
UK
www.iste.co.uk
Elsevier Ltd
The Boulevard, Langford Lane
Kidlington, Oxford, OX5 1GB
UK
www.elsevier.com
Notices
Knowledge and best practice in this field are constantly changing. As new research and experience broaden our understanding, changes in research methods, professional practices, or medical treatment may become necessary.
Practitioners and researchers must always rely on their own experience and knowledge in evaluating and using any information, methods, compounds, or experiments described herein. In using such information or methods they should be mindful of their own safety and the safety of others, including parties for whom they have a professional responsibility.
To the fullest extent of the law, neither the Publisher nor the authors, contributors, or editors, assume any liability for any injury and/or damage to persons or property as a matter of products liability, negligence or otherwise, or from any use or operation of any methods, products, instructions, or ideas contained in the material herein.
For information on all our publications visit our website at http://store.elsevier.com/
ISTE Press Ltd 2018
The rights of Dominique P. Chevallier and Jean Lerbet to be identified as the authors of this work have been asserted by them in accordance with the Copyright, Designs and Patents Act 1988.
British Library Cataloguing-in-Publication Data
A CIP record for this book is available from the British Library
Library of Congress Cataloging in Publication Data
A catalog record for this book is available from the Library of Congress
ISBN 978-1-78548-231-1
Printed and bound in the UK and US
List of Notations
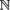 set of integers
set of integers
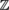 ring of rational integers
ring of rational integers
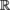 real number field
real number field
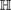 real quaternion field (Appendix 1 to )
real quaternion field (Appendix 1 to )
dual number ring (see )
dual number such that 2 = 0 (see )
Df differential of the map f (see )
f T tangent map of the map f (see )
symbol of the composition of maps
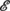 Euclidean affine space (generally of dimension 3)
Euclidean affine space (generally of dimension 3)
Tr ( u ) translation in 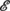 by the vector uE
by the vector uE 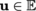 (see )
(see )
E 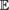 vector space (very often the Euclidean of dimension 3 over
vector space (very often the Euclidean of dimension 3 over 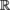 )
)
vector product (or cross product) in the oriented dimension 3 Euclidean vector space
mapping x a x in the oriented dimension 3 Euclidean vector space
[ | ] Lie bracket in a Lie algebra
(; ; ) mixed product in the dimension 3 Euclidean vector space
{ | } dual mixed product in the -module D 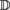 (see )
(see )
{; ; } dual mixed product in the -module D 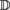 (see )
(see )
E 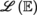 algebra of the linear operators in the vector space E
algebra of the linear operators in the vector space E 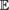 (see )
(see )
GlE 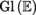 group of the regular linear operators the vector space E
group of the regular linear operators the vector space E 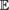 (see )
(see )
OE 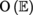 Orthogonal group of the Euclidean vector space E
Orthogonal group of the Euclidean vector space E 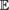 (see )
(see )
SOE 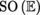 Special othogonal group of the Euclidean vector space E
Special othogonal group of the Euclidean vector space E 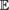 (see )
(see )
U 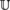 group of the normalized quaternions
group of the normalized quaternions
Ga 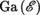 group of affine transformations of
group of affine transformations of 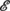
D,D 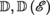 Displacement group of
Displacement group of 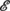
D,D 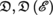 Lie algebra of D
Lie algebra of D 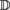 (of the skewsymmetric vectorfields on
(of the skewsymmetric vectorfields on 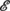 see )
see )
| Klein form of D 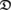 (see )
(see )
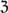 set of vector fields DT
set of vector fields DT 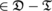 vanishing on their axe (see )
vanishing on their axe (see )
a 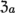














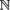 set of integers
set of integers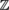 ring of rational integers
ring of rational integers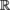 real number field
real number field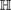 real quaternion field (Appendix 1 to )
real quaternion field (Appendix 1 to )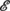 Euclidean affine space (generally of dimension 3)
Euclidean affine space (generally of dimension 3)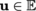 (see )
(see )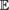 vector space (very often the Euclidean of dimension 3 over
vector space (very often the Euclidean of dimension 3 over 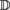 (see )
(see )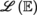 algebra of the linear operators in the vector space E
algebra of the linear operators in the vector space E 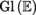 group of the regular linear operators the vector space E
group of the regular linear operators the vector space E 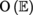 Orthogonal group of the Euclidean vector space E
Orthogonal group of the Euclidean vector space E 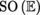 Special othogonal group of the Euclidean vector space E
Special othogonal group of the Euclidean vector space E 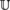 group of the normalized quaternions
group of the normalized quaternions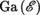 group of affine transformations of
group of affine transformations of 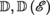 Displacement group of
Displacement group of 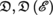 Lie algebra of D
Lie algebra of D 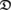 (see )
(see )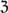 set of vector fields DT
set of vector fields DT 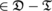 vanishing on their axe (see )
vanishing on their axe (see )