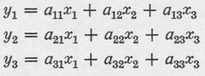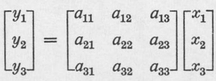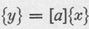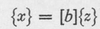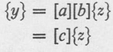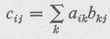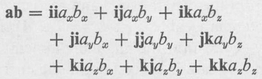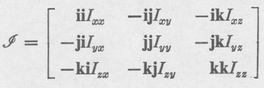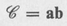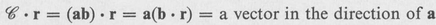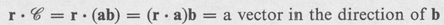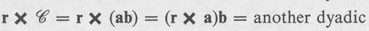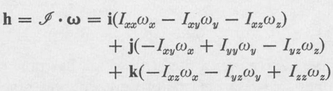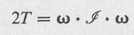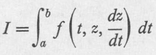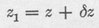William Tyrrell Thomson - Introduction to Space Dynamics

A system of linear equations

(A1)

can be arranged into the matrix notation

(A2)

where the rule for the matrix multiplication is evident from the original equations. For Eq. A2 to equal Eq. A1, the terms of each row must be multiplied by the terms of the column x1, x2, x3. We can then view the matrix equation, Eq. A2, as a convenient notation which may be further abbreviated to

(A3)

We will next consider another set of linear equations like that of Eq. A1, relating x to z , and write its matrix form as

(A4)

where [ b ] is a square matrix like that of Eq. A2. If we wish to relate y to z , Eq. A4 can be substituted into Eq. A3 as follows:

(A5)

The elements of [c] can then be shown to be available from the equation

(A6)

i.e., the third element of the second row is

c 23 = a 21 b 13 + a 22 b 23 + a 23 b 33

There are many theorems relating to the manipulation of matrix equations; however for the purposes of linear transformation of coordinates, as treated in this text, the simple algebraic concepts discussed above are sufficient.

We occasionally encounter a quantity which has nine components in a threedimensional space. In elasticity we encounter nine components of stress at a point, whereas in dynamics we find nine components of inertia.

For our purposes we can define a dyadic as a ninecomponent quantity which can be formed by multiplying two vectors, ignoring the dotor crossproduct rule. Thus the product of two vectors a and b is,

(B1)

Although the above dyadic was formed by the multiplication of the two vectors a and b, the elements of the dyadic (called dyads) need not be related to the two vectors. Furthermore, it is convenient to arrange such terms in matrix form, so that a dyadic is in general expressible as,

(B2)

As an example of a dyadic not related to any vector, we have the inertia dyadic,

(B3)

To illustrate the general rule for the dot or cross product of a dyadic with a vector, we assume that the dyadic is formed by the product of two vectors as

(B4)

Its dot and cross product with a vector r is then dependent on the order of the product, and its interpretation is made clear by the following examples:

(B5)

(B6)

(B7)

(B8)

If we form the dot product of the inertia dyadic with the angular velocity vector = x i + y j + z k , the result will be the angular momentum vector.

(B9)

Here we encounter dot products such as,

ji i = j ( i i ) = j
ji j = j ( i j ) = 0, etc.

which are evident from the general rule, and recognize that the subscripts of the inertia are interchangeable, i.e., I xy = I yx . If, furthermore, we dot the angular velocity vector into the angular momentum vector, the result is a scalar, which in this case is twice the kinetic energy.

(B10)

In summary, the dyadic is a special form of a tensor; however, our simple definition of the dyadic and its product with a vector requires no new rules of vector algebra, which appears to be adequate for the dynamical problems encountered in this text. For further reading on the subject, see reference.

Many problems in Dynamics are formulated in terms of maxima and minima of quantities expressed by an integral. In this section we will briefly discuss the essentials of the variational calculus which are encountered for such problems.

Consider the integral,

(C1)

taken along a curve z = ( t ). The quantity z can stand for any number of variables, such as position x , y , and the thrust attitude of the missile problem. The value of the integral I will depend on the curve z = ( t ) which we wish to find for the condition of maxima or minima of the integral C1.

Assuming that z = ( t ) along curve ab of to be the optimum curve, we draw curve 1 along ab 1 as the varied curve. The quantity z along the varied curve is represented by