ROTATING FLUIDS
IN ENGINEERING
AND SCIENCE
James P. Vanyo
Department of Mechanical and Environmental Engineering
Department of Geological Sciences
University of California, Santa Barbara
DOVER PUBLICATIONS, INC.
Mineola, New York
Copyright
Copyright 1993 by James P. Vanyo
All rights reserved.
Bibliographical Note
This Dover edition, first published in 2001, is an unabridged reprint of the work originally published by Butterworth-Heinemann, Stoneham, Mass., in 1993.
Library of Congress Cataloging-in-Publication Data
Vanyo, James P.
Rotating fluids in engineering and science / James P. Vanyo.
p. cm.
Includes bibliographical references and index.
eISBN 13: 978-0-486-16198-3
1. Fluid mechanics. 2. Rotating masses of fluids. I. Title.
TA357 .V36 2001
620.1'06dc21
2001017222
Manufactured in the United States by Courier Corporation
41704202
www.doverpublications.com
Preface
Rotating Fluids in Engineering and Science was written to help make rotating fluid phenomena more accessible to students and researchers in the field of fluid mechanics. The book is designed to be used as an upper-division text and/or beginning graduate text. It is also intended for practicing engineers and scientists engaged in research or in design and development projects requiring a knowledge of rotating fluid theory. The book leads the reader systematically through rotating flow theory and applications, and shows that the theory and applications can be mastered easily by students and practicing professionals. It is hoped that the text will help bridge the gap between undergraduate preparation in fluid mechanics, and the understanding needed to benefit from professional journal articles and more advanced monographs in this field.
The reader is assumed to be familiar with partial differential equations and vector mathematics, although important parts of these are reviewed in includes solved quantitative examples.
includes a list of suggested projects and study assignments for groups and/or individuals. They vary in difficulty and type; some are analytical while others are numerical or experimental.
Constant density and viscosity flows are emphasized, although thermal and compressibility phenomena are included. Data and quantitative examples are presented in both dimensional and nondimensional forms. Most dimensional quantities are expressed in SI and cgs units, although other units commonly seen in U.S. applications are also illustrated, e.g., ft, lbf, psi, gpm, and mph. A table of conversion factors is included in conventions. Vectors are printed in bold face characters, e.g., V is vector velocity, V is scalar speed, and unit vectors are designated with a caret, e.g., 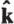 . The author combines laboratory demonstrations and student projects with lectures. The text continues this format by including experimental and practical results to support discussions of theory. It also includes references to advanced texts and journals as an aid in formulating professional level research projects.
. The author combines laboratory demonstrations and student projects with lectures. The text continues this format by including experimental and practical results to support discussions of theory. It also includes references to advanced texts and journals as an aid in formulating professional level research projects.
The University of California, Santa Barbara, follows a quarter system of instruction, ten lecture weeks followed by an examination week. As an undergraduate text for students who have completed a two quarter fluids sequence, the author devotes one week to Rotating Fluid Applications. The emphasis is on helping students make the transition from an undergraduate pattern of weekly, precisely defined, homework problem sets to a more professional level, i.e., applying theory to open-ended complex problem areas, often including a need to make reasonable approximations to achieve success.
Several quizzes during the first 6 weeks, rather than homework sets, are used to promote knowledge of relevant theory and equations; these are followed by individual or small group projects selected/assigned from is covered as review, and the text is augmented with additional source material from professional journals and advanced monographs.
Rotating Fluids in Engineering and Science was developed over the last 22 years by the author at the University of California, Santa Barbara. The format and content of the text, as it developed, was in response to, and aided by discussions with, the many students who have taken my courses on rotating fluids or who assisted with laboratory projects. Two students, R. Hadley and S. Stojanovich, checked solutions for many of the example problems in . 5. McLean assisted by reviewing material on oceanography, and L. Pauley made other valuable suggestions.
I want to thank all contributors for their help; the editorial staff and reviewers of Butterworth-Heinemann for their guidance; and I especially wish to thank Christine Townsley for the many, many hours of careful, patient, and cheerful assistance in typing several preliminary drafts, and finally in preparing the text in camera-ready form.
Professor James P. Vanyo
University of California
Santa Barbara
PART I
Fluid Mechanics Review
Chapter 1
Rotating Fluid Phenomena
Many areas of engineering and science involve the rotation of various objects; in science the object sometimes is the earth; in engineering it might be a turbine rotor or a space vehicle. In most cases the object also involves the rotation of internal or external fluids. Sometimes a rotating fluid is the principal phenomena of interest; at other times the fluid is merely an unwanted participant in the motion. In either event, success or failure of the analysis can depend critically on understanding and predicting rotating fluid phenomena.
The basic theory of fluid rotation and vorticity distinguishes between vorticity and curved (e.g., circular) translation of fluid elements..
shows water in a cylinder. In the left photograph, both the cylinder and the water are stationary, and all the colored water, slightly less dense than the clear water, is in the top one-eighth of the cylinder. In the right photograph, the cylinder has been impulsively accelerated to a constant angular velocity, and the water is gradually being "spun up" to the angular velocity of the cylinder. Liquid spin-up is achieved about 1% by viscous interaction at the cylinder side walls and about 99% by a viscous secondary flow at the cylinder bottom. Centrifugal force inside this very thin (almost invisible) spinning bottom boundary layer moves clear water outward and then up along the outside cylinder wall. Colored water in the interior is drawn downward until all the water will be pumped outward through the very thin, bottom boundary layer. In this experiment, a 2% buoyancy of the colored water is opposing the pumping action and causes the boundary between the clear and colored water to be tapered rather than cylindrical. More complex rotating fluid phenomena, such as internal waves and vortex stretching, are involved during a reverse spin-down process.
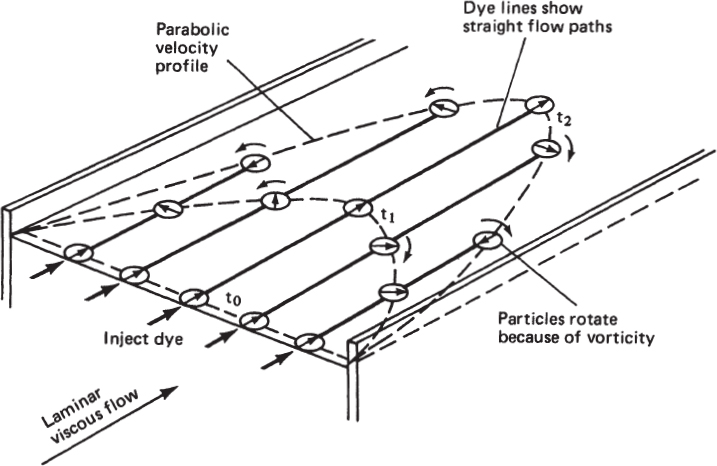
Figure 1.1: Laminar flow of a viscous fluid in a straight channel moves along straight streamlines. The fluid elements rotate, however, because of viscosity. The streamlines can be observed by injecting ink into the flow, and the rotation (vorticity) can be observed by the rotation of small corks placed in the flow.
Rotating masses of fluid exhibit other unusual properties. shows the difference between flow patterns created by suddenly dumping a quantity of similar density colored water into nonrotating water, (top two photographs), and flow patterns created by the same act, but using rotating water as shown in the bottom two photographs. Typical turbulent eddies are generated in the nonrotating water. Such random motions are not possible in a rotating liquid; instead, permissible flows have a distinctly two-dimensional property as shown in the photographs.










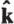 . The author combines laboratory demonstrations and student projects with lectures. The text continues this format by including experimental and practical results to support discussions of theory. It also includes references to advanced texts and journals as an aid in formulating professional level research projects.
. The author combines laboratory demonstrations and student projects with lectures. The text continues this format by including experimental and practical results to support discussions of theory. It also includes references to advanced texts and journals as an aid in formulating professional level research projects.