Table of Contents
List of Tables
- Chapter 01
- Chapter 02
- Chapter 05
- Chapter 13
List of Illustrations
- Chapter 05
- Chapter 01
- Chapter 02
- Chapter 03
- Chapter 04
- Chapter 05
- Chapter 06
- Chapter 07
- Chapter 08
- Chapter 09
- Chapter 10
- Chapter 11
- Chapter 12
- Chapter 13
Guide
Pages
Physicochemical Fluid Dynamics in Porous Media
Applications in Geosciences and Petroleum Engineering
Mikhail Panfilov
Copyright
Author
Prof. Mikhail Panfilov
Institute Elie Cartan - University of Lorraine
CNRS
bd. Aguillettes, BP 70239
54506, Vandoeuvre-ls-Nancy
France
Institute Jean le Rond 'Alembert - Sorbonne University CNRS
4, Place Jussieu, BP 162
75252 Paris
France
All books published by Wiley-VCH are carefully produced. Nevertheless, authors, editors, and publisher do not warrant the information contained in these books, including this book, to be free of errors. Readers are advised to keep in mind that statements, data, illustrations, procedural details or other items may inadvertently be inaccurate.
Library of Congress Card No.: applied for
British Library Cataloguing-in-Publication Data
A catalogue record for this book is available from the British Library.
Bibliographic information published by the Deutsche Nationalbibliothek
The Deutsche Nationalbibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data are available on the Internet at http://dnb.d-nb.de.
2019 Wiley-VCH Verlag GmbH & Co. KGaA, Boschstr. 12, 69469 Weinheim, Germany
All rights reserved (including those of translation into other languages). No part of this book may be reproduced in any form by photoprinting, microfilm, or any other means nor transmitted or translated into a machine language without written permission from the publishers. Registered names, trademarks, etc. used in this book, even when not specifically marked as such, are not to be considered unprotected by law.
Print ISBN: 978-3-527-34235-8
ePDF ISBN: 978-3-527-80656-0
ePub ISBN: 978-3-527-80658-4
oBook ISBN: 978-3-527-80657-7
Preface
This book is the general theory that analyzes all types of flows and transport coupled with chemical, physicochemical, or biochemical phenomena, such as the dissolution of species in different phases, chemical reactions, chemical adsorption, molecular diffusion, capillarity, surface phenomena, movement of menisci and films, and reactions induced by microorganisms and bacterial dynamics.
These processes are considered at different scales, from a pore through a pore network to the macroscopic level called Darcy's scale. Different methods of analysis are applied on different scales: method of diffuse interface, lubrication approximation, asymptotic analysis, methods of Markov stochastic processes, and percolation methods. On the macroscopic scale, these various processes are considered on the same mathematical basis, which may be reduced to canonical models of kinematic waves. The analysis of biochemical flow is based on the methods of dynamical systems and nonlinear reactiondiffusion equations. The qualitative physical analysis is based on the development of analytical or semianalytical solutions of fundamental problems related to various engineering applications. Among them, I pay particular attention to the processes of enhanced oil recovery (injection of miscible gases, surfactants, polymers, microbiological enhanced oil recovery ( EOR )), underground storage of gas (hydrogen, CO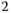 , methane), and underground leaching of uranium and rare elements. The book also contains the thermodynamics of phase equilibria for multicomponent fluids, which is the main tool for describing the chemical processes of species dissolution and phase transition. The presentation contains both classical parts and new results that are being published for the first time in a monograph.
, methane), and underground leaching of uranium and rare elements. The book also contains the thermodynamics of phase equilibria for multicomponent fluids, which is the main tool for describing the chemical processes of species dissolution and phase transition. The presentation contains both classical parts and new results that are being published for the first time in a monograph.
The book is aimed at scientists, students, and engineers working in the domain of fluid mechanics, applied mathematics, chemistry, microbiology, thermodynamics, reservoir engineering, and geology.
The idea of writing such a book that would demonstrate how to link thermodynamics, chemistry, biochemistry and hydrodynamics into unified mathematical models and how to carry out their qualitative mathematical analysis, arose in 20062007, when I lectured on this topic at the Poincar Institute in Paris at the invitation of the French mathematicians Alain Bourgat, Gregoire Allaire, Andro Mikelic, Brahim Amaziane, Roland Masson and other. They inspired me and convinced that such a book could be useful.
I dedicate it to them, to French mathematicians.
Nancy, Paris, France
January 19, 2018
Mikhail Panfilov
Introduction
1 Structure of a Heterogeneous Fluid
The physicochemical fluid dynamic s ( PCFD ) studies the motion of a heterogeneous fluid that consists of several chemical species, which can interact chemically with each other. All the species may be separated into two classes: the phases and the chemical components. The phases are separated by the interfaces, while the chemical components are mixed on the molecular scale and do not create any interface between them. Any system analyzed in this book is at least twophase and contains one or two fluids and a solid in the form of a porous medium.
In other words, phases form a macroscopic structure of the fluid, while components determine its microscopic structure.
One distinguishes three classes of heterogeneous fluids:
- Immiscible: The fluid contains interfaces, which are impenetrable for chemical components present in the phases; such a system is multiphase.
- Completely miscible (the solutions): They are singlephase; no interface between the fluid components exists.
- Partially miscible: The fluid contains interfaces (and phases), but they are penetrable for chemical components.
Each component of a multicomponent mixture occupies the total volume. Each phase of a multiphase system occupies only a part of the volume. Consequently, the phases may be identified by their specific volumes or volume fractions. The volume fraction occupied by the overall fluid is called porosity. The volume fraction of a phase with respect to the total volume of the fluid is called saturation. For chemical components, the volume fractions have no meaning (they are all equal to 1); this is why they are identified by molar or mass fractions. They are defined as follows for any component 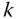 :
:
(1.1)
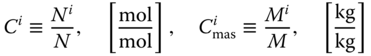
where 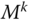









 , methane), and underground leaching of uranium and rare elements. The book also contains the thermodynamics of phase equilibria for multicomponent fluids, which is the main tool for describing the chemical processes of species dissolution and phase transition. The presentation contains both classical parts and new results that are being published for the first time in a monograph.
, methane), and underground leaching of uranium and rare elements. The book also contains the thermodynamics of phase equilibria for multicomponent fluids, which is the main tool for describing the chemical processes of species dissolution and phase transition. The presentation contains both classical parts and new results that are being published for the first time in a monograph. :
: