
Copyright 2017 by John Wiley & Sons, Inc. All rights reserved
Published simultaneously in Canada
Published by John Wiley & Sons, Inc., Hoboken, New Jersey
No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 750-4470, or on the web at www.copyright.com. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008, or online at http://www.wiley.com/go/permission.
Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representations or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives or written sales materials. The advice and strategies contained herein may not be suitable for your situation. You should consult with a professional where appropriate. Neither the publisher nor author shall be liable for any loss of profit or any other commercial damages, including but not limited to special, incidental, consequential, or other damages.
For general information on our other products and services or for technical support, please contact our Customer Care Department within the United States at (800) 762-2974, outside the United States at (317) 572-3993 or fax (317) 572-4002.
Wiley also publishes its books in a variety of electronic formats. Some content that appears in print may not be available in electronic formats. For more information about Wiley products, visit our web site at www.wiley.com.
Library of Congress Cataloging-in-Publication Data:
Names: Lorenzo, Carl F. | Hartley, T. T. (Tom T.), 1964
Title: The fractional trigonometry : with applications to fractional differential equations and science / Carl F. Lorenzo, National Aeronautics and Space Administration, Glenn Research Center, Cleveland, Ohio, Tom T.
Hartley, The University of Akron, Akron, Ohio.
Description: Hoboken, New Jersey : John Wiley & Sons, Inc., [2017] | Includes bibliographical references and index.
Identifiers: LCCN 2016027837 (print) | LCCN 2016028337 (ebook) | ISBN 9781119139409 (cloth) | ISBN 9781119139423 (pdf) | ISBN 9781119139430 (epub)
Subjects: LCSH: Fractional calculus. | Trigonometry.
Classification: LCC QA314 .L67 2017 (print) | LCC QA314 (ebook) | DDC 516.24-dc23
LC record available at https://lccn.loc.gov/2016027837
Preface
There has been a strong resurgence of interest in the fractional calculus over the last two or three decades. This expansion of the classical calculus to derivatives and integrals of fractional order has given rise to the hope of a new understanding of the behavior of the physical world. The hope is that problems that have resisted solution by the integer-order calculus will yield to this greatly expanded capability. As a result of our work in the fractional calculus, and more particularly, in functions for the solutions of fractional differential equations, an interest was fostered in the behavior of generalized exponential functions for this application. Our work with the fundamental fractional differential equation had developed a function we named the F-function. This function, which had previously been mentioned in a footnote by Oldham and Spanier, acts as the fractional exponential function. It was a natural step from there to an interest in a fractional trigonometry. At that time, only a few pages of work were available in the literature and were based on the Mittag-Leffler function. These are shown in Appendix A.
This book brings together our research in this area over the past 15 years and adds much new unpublished material.
The classical trigonometry plays a very important role relative to the integer-order calculus; that is, it, together with the common exponential function, provides solutions for linear differential equations. We will find that the fractional trigonometry plays an analogous role relative to the fractional calculus by providing solutions to linear fractional differential equations. The importance of the classical trigonometry goes far beyond the solutions of triangles. Its use in Fourier integrals, Fourier series, signal processing, harmonic analysis, and more provided great motivation for the development of a fractional trigonometry to expand application to the fractional calculus domain.
Because we are engineers, this book has been written in the style of the engineering mathematical books rather than the more rigorous and compact style of definition, theorem, and proof, found in most mathematical texts. We, of course, have made every effort to assure the derivations to be correct and are hopeful that the style has made the material accessible to a larger audience. We are also hopeful that this will not detract the interest of the mathematical community in the area since their skills will be needed to develop this important new area. Most of the materials of this book should be accessible to an undergraduate student with a background in Laplace transforms.
After an introductory chapter, which offers a brief insight into the fractional calculus, the book is organized in two major parts. In provide insight into various areas of potential application.
further develops properties of the R-function that expose the character of this fractional exponential function.
In .
develops the R1-trigonometry. It is based on the R-function with imaginary parameter a, namely 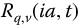 . Multiplication of the parameter by i toggles the R1-hyperbolic functions to the R1-trigonometric functions, and so on.
. Multiplication of the parameter by i toggles the R1-hyperbolic functions to the R1-trigonometric functions, and so on.
A fractional trigonometry, the R2-trigonometry based on an imaginary time variable, 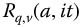 , is developed in . It is found that these functions are characterized by their attraction to circles when plotted in phase plane format.
, is developed in . It is found that these functions are characterized by their attraction to circles when plotted in phase plane format.
The obvious extension of these two trigonometries, the R3-trigonometry of , sets both the a parameter and the t variable to be imaginary, 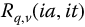 . It was thought at the time that this trigonometry would behave as an hyperbolic analog to the R2-trigonometry. However, such simple relationships between the two were not found.
. It was thought at the time that this trigonometry would behave as an hyperbolic analog to the R2-trigonometry. However, such simple relationships between the two were not found.
presents the heart of the fractional trigonometry, namely the fractional meta-trigonometry. Here, both a and t are allowed to be fully complex, by choosing as the basis 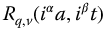 . This chapter generalizes the results of the previous four chapters. Laplace transforms for the generalized functions are determined along with their fractional differintegrals. Fractional exponential forms for the functions are also determined.
. This chapter generalizes the results of the previous four chapters. Laplace transforms for the generalized functions are determined along with their fractional differintegrals. Fractional exponential forms for the functions are also determined.
Next page




















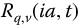 . Multiplication of the parameter by i toggles the R1-hyperbolic functions to the R1-trigonometric functions, and so on.
. Multiplication of the parameter by i toggles the R1-hyperbolic functions to the R1-trigonometric functions, and so on.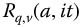 , is developed in . It is found that these functions are characterized by their attraction to circles when plotted in phase plane format.
, is developed in . It is found that these functions are characterized by their attraction to circles when plotted in phase plane format.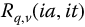 . It was thought at the time that this trigonometry would behave as an hyperbolic analog to the R2-trigonometry. However, such simple relationships between the two were not found.
. It was thought at the time that this trigonometry would behave as an hyperbolic analog to the R2-trigonometry. However, such simple relationships between the two were not found.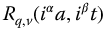 . This chapter generalizes the results of the previous four chapters. Laplace transforms for the generalized functions are determined along with their fractional differintegrals. Fractional exponential forms for the functions are also determined.
. This chapter generalizes the results of the previous four chapters. Laplace transforms for the generalized functions are determined along with their fractional differintegrals. Fractional exponential forms for the functions are also determined.