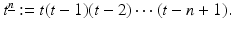Christopher Goodrich - Discrete Fractional Calculus
Here you can read online Christopher Goodrich - Discrete Fractional Calculus full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2016, publisher: Springer, genre: Science. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Discrete Fractional Calculus
- Author:
- Publisher:Springer
- Genre:
- Year:2016
- Rating:4 / 5
- Favourites:Add to favourites
- Your mark:
Discrete Fractional Calculus: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Discrete Fractional Calculus" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
This text provides the first comprehensive treatment of the discrete fractional calculus. Experienced researchers will find the text useful as a reference for discrete fractional calculus and topics of current interest. Students who are interested in learning about discrete fractional calculus will find this text to provide a useful starting point. Several exercises are offered at the end of each chapter and select answers have been provided at the end of the book.
The presentation of the content is designed to give ample flexibility for potential use in a myriad of courses and for independent study. The novel approach taken by the authors includes a simultaneous treatment of the fractional- and integer-order difference calculus (on a variety of time scales, including both the usual forward and backwards difference operators). The reader will acquire a solid foundation in the classical topics of the discrete calculus while being introduced to exciting recent developments, bringing them to the frontiers of the subject.
Most chapters may be covered or omitted, depending upon the background of the student. For example, the text may be used as a primary reference in an introductory course for difference equations which also includes discrete fractional calculus. Chapters 12 provide a basic introduction to the delta calculus including fractional calculus on the set of integers. For courses where students already have background in elementary real analysis, Chapters 12 may be covered quickly and readers may then skip to Chapters 67 which present some basic results in fractional boundary value problems (FBVPs). Chapters 67 in conjunction with some of the current literature listed in the Bibliography can provide a basis for a seminar in the current theory of FBVPs. For a two-semester course, Chapters 15 may be covered in depth, providing a very thorough introduction to both the discrete fractional calculus as well as the integer-order calculus.Christopher Goodrich: author's other books
Who wrote Discrete Fractional Calculus? Find out the surname, the name of the author of the book and a list of all author's works by series.









![Chris Monahan [Chris Monahan] - Calculus II](/uploads/posts/book/119088/thumbs/chris-monahan-chris-monahan-calculus-ii.jpg)




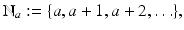
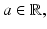 or a set of the form
or a set of the form 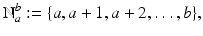
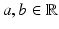 and b a is a positive integer.
and b a is a positive integer.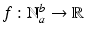 . If b > a , then we define the forward difference operator
. If b > a , then we define the forward difference operator 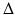 by
by 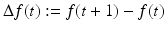
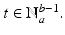
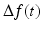 , as we shall do throughout this text. Technically, it would be more precise to write
, as we shall do throughout this text. Technically, it would be more precise to write 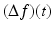 to emphasize that
to emphasize that 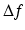 is a function that is being evaluated at the point t . However, as long as one understands this true meaning of the notation, then we see no harm in using the simpler-to-read notation
is a function that is being evaluated at the point t . However, as long as one understands this true meaning of the notation, then we see no harm in using the simpler-to-read notation 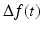 .
.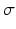 on
on 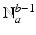 by
by 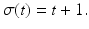
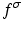 to denote the function defined by the composition
to denote the function defined by the composition 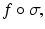 that is
that is 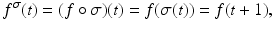
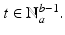 Also, the operator
Also, the operator 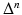 ,
, 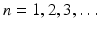 is defined recursively by
is defined recursively by 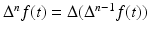 for
for 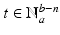 , where we assume the integer b a n .Finally,
, where we assume the integer b a n .Finally, 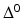 denotes the identity operator, i.e.,
denotes the identity operator, i.e., 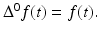
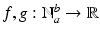 and
and 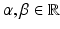 , then for
, then for 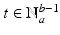
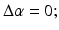
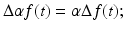
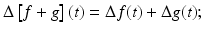
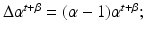
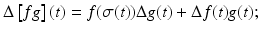
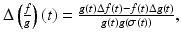
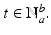
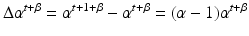
 is a linear operator .
is a linear operator .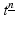 , read t to the n falling, by
, read t to the n falling, by