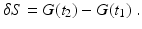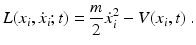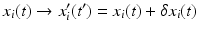1. Introduction
The subject of this monograph is classical and quantum dynamics. We are fully aware that this combination is somewhat unusual, for history has taught us convincingly that these two subjects are founded on totally different concepts; a smooth transition between them has so far never been made and probably never will.
An approach to quantum mechanics in purely classical terms is doomed to failure; this fact was well known to the founders of quantum mechanics. Nevertheless, to this very day people are still trying to rescue as much as possible of the description of classical systems when depicting the atomic world. However, the currently accepted viewpoint is that in describing fundamental properties in quantum mechanics, we are merely borrowing names from classical physics. In writing this book we have made no attempt to contradict this point of view. But in the light of modern topological methods we have tried to bring a little twist to the standard approach that treats classical and quantum physics as disjoint subjects.
The formulation of both classical and quantum mechanics can be based on the principle of stationary action. Schwinger has advanced this principle into a powerful working scheme which encompasses almost every situation in the classical and quantum worlds. Our treatment will give a modest impression of the wide range of applicability of Schwingers action principle.
We then proceed to rediscover the importance of such familiar subjects as Jacobi fields, action angle variables, adiabatic invariants, etc. in the light of current research on classical Hamiltonian dynamics. It is here that we recognize the important role that canonical perturbation theory played before the advent of modern quantum mechanics.
Meanwhile, classical mechanics has been given fresh impetus through new developments in perturbation theory, offering a new look at old problems in nonlinear mechanics like, e.g., the stability of the solar system. Here the KAM theorem proved that weakly disturbed integrable systems will remain on invariant surfaces (tori) for most initial conditions and do not leave the tori to end up in chaotic motion.
At this stage we point to the fundamental role that adiabatic invariants played prior to canonical quantization of complementary dynamical variables. We are reminded of torus quantization, which assigns each adiabatic invariant an integer multiple of Plancks constant. All these semiclassical quantization procedures have much in common with Feynmans path integral or, rather, approximations thereof. Indeed, Feynmans path integral methods are ideally suited to follow a quantum mechanical systemif certain restrictions are enforcedinto its classical realm. Consequently it is one of our main goals to apply Feynmans path integral and other geometrical methods to uncover the mystery of the zero point energy (Maslov anomaly) of the quantum harmonic oscillator.
That quantum and classical mechanics are, in fact, disjoint physical worlds was clear from the very beginning. Present-day experience is no exception; it is rather embarrassing to find out that an important geometric phase in a cyclic adiabatic quantal process has been overlooked since the dawn of quantum mechanics. This so-called Berry phase signals that in nonrelativistic as well as relativistic quantum theory, geometrical methods play an eminent role.
The appearance of topology in quantum mechanics is probably the most important new development to occur in recent years. A large portion of this text is therefore devoted to the geometric structure of topologically nontrivial physical systems. Berry phases, Maslov indices, ChernSimons terms and various other topological quantities have clearly demonstrated that quantum mechanics is not, as of yet, a closed book.
2. The Action Principles in Mechanics
We begin this chapter with the definition of the action functional as time integral over the Lagrangian
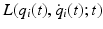
of a dynamical system:
Here, q i , i =1,2,, N , are points in N -dimensional configuration space. Thus q i ( t ) describes the motion of the system, and
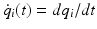
determines its velocity along the path in configuration space. The endpoints of the trajectory are given by q i ( t 1)= q i 1, and q i ( t 2)= q i 2.
Next we want to find out what the actual dynamical path of the system is. The answer is contained in the principle of stationary action: in response to infinitesimal variation of the integration path, the action S is stationary, S =0, for variations about the correct path, provided the initial and final configurations are held fixed. On the other hand, if we permit infinitesimal changes of q i ( t ) at the initial and final times, including alterations of those times, the only contribution to S comes from the endpoint variations, or
Equation () is the most general formulation of the action principle in mechanics. The fixed values G 1 and G 2 depend only on the endpoint path variables at the respective terminal times.
Again, given a system with the action functional S , the actual time evolution in configuration space follows that path about which general variations produce only endpoint contributions. The explicit form of G is dependent upon the special representation of the action principle. In the following we begin with the one that is best known, i.e.,
1. Lagrange:
The Lagrangian for a point particle with mass m , moving in a potential V ( x i , t ), is
Here and in the following we restrict ourselves to the case N =3; i.e., we describe the motion of a single mass point by x i ( t ) in real space. The dynamical variable x i ( t ) denotes the actual classical trajectory of the particle which is parametrized by t with t 1 t t 2.
Now we consider the response of the action functional () with respect to changes in the coordinates and in the time, x i ( t ) and t ( t ), respectively. It is important to recognize that, while the original trajectory is being shifted in real space according to
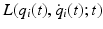 of a dynamical system:
of a dynamical system: 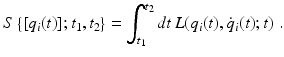
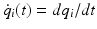 determines its velocity along the path in configuration space. The endpoints of the trajectory are given by q i ( t 1)= q i 1, and q i ( t 2)= q i 2.
determines its velocity along the path in configuration space. The endpoints of the trajectory are given by q i ( t 1)= q i 1, and q i ( t 2)= q i 2.