1.1 Feature Extraction
Pattern recognition and data compression are two applications that rely critically on efficient data representation []. In these applications, it is desirable to extract measurements that are invariant or insensitive to the variations within each class. The process of extracting such measurements is called feature extraction . It is also to say feature extraction is a data processing which maps a high-dimensional space to a low-dimensional space with minimum information loss.
Principal component analysis (PCA) is a well-known feature extraction method, while minor component analysis (MCA) and independent component analysis (ICA) can be regarded as variants or generalizations of the PCA. MCA is most useful for solving total least squares (TLS) problems, and ICA is usually used for blind signal separation (BSS).
In the following, we briefly review PCA, PCA neural networks, and extensions or generalizations of PCA.
1.1.1 PCA and Subspace Tracking
The principal components (PC) are the directions in which the data have the largest variances and capture most of the information contents of data. They correspond to the eigenvectors associated with the largest eigenvalues of the autocorrelation matrix of the data vectors. Expressing data vectors in terms of the PC is called PCA. On the contrary, the eigenvectors that correspond to the smallest eigenvalues of the autocorrelation matrix of the data vectors are defined as the minor components (MC), and MC are the directions in which the data have the smallest variances (they represent the noise in the data). Expressing data vectors in terms of the MC is called MCA. Now, PCA has been successfully applied in many data processing problems, such as high-resolution spectral estimation, system identification, image compression, and pattern recognition, and MCA is also applied in total least squares, moving target indication, clutter cancelation, curve and surface fitting, digital beamforming, and frequency estimation.
The PCA or MCA is usually one dimensional. However, in real applications, PCA or MCA is mainly multiple dimensional. The eigenvectors associated with the r largest (or smallest) eigenvalues of the autocorrelation matrix of the data vectors is called principal (or minor) components, and r is referred to as the number of the principal (or minor) components. The eigenvector associated with the largest (smallest) eigenvalue of the autocorrelation matrix of the data vectors is called largest (or smallest) component. The subspace spanned by the principal components is called principal subspace (PS), and the subspace spanned by the minor components is called minor subspace (MS). In some applications, we are only required to find the PS (or MS) spanned by r orthonormal eigenvectors. The PS is sometimes called signal subspace, and the MS is called noise subspace. Principal and minor component analyzers of a symmetric matrix are matrix differential equations that converge on the PCs and MCs, respectively. Similarly, the principal (PSA) and minor (MSA) subspace analyzers of a symmetric matrix are matrix differential equations that converge on a matrix whose columns span is the PS and MS, respectively. PCA/PSA and MCA/MSA are powerful techniques in many information processing fields. For example, PCA/PSA is a useful tool in feature extraction, data compression, pattern recognition, and time series prediction [].
As discussed before, the PC is the direction which corresponds to the eigenvector associated with the largest eigenvalue of the autocorrelation matrix of the data vectors, and the MC is the direction which corresponds to the eigenvector associated with the smallest eigenvalue of the autocorrelation matrix of the data vectors. Thus, implementations of these techniques can be based on batch eigenvalue decomposition (ED) of the sample correlation matrix or on singular value decomposition (SVD) of the data matrix. This approach is unsuitable for adaptive processing because it requires repeated ED/SVD, which is a very time-consuming task []. Thus, the attempts to propose adaptive algorithms are still continuing even though the field has been active for three decades up to now.
1.1.2 PCA Neural Networks
In order to overcome the difficulty faced by ED or SVD, a number of adaptive algorithms for subspace tracking were developed in the past. Most of these techniques can be grouped into three classes [] have been proposed to track the signal or noise subspace.
Neural network approaches on PCA or MCA pursue an effective online approach to update the eigen direction after each presentation of a data point, which possess many obvious advantages, such as lower computational complexity, compared with the traditional algebraic approaches such as SVD. Neural network methods are especially suited for high-dimensional data, since the computation of the large covariance matrix can be avoided, and for the tracking of nonstationary data, where the covariance matrix changes slowly over time. The attempts to improve the methods and to suggest new approaches are continuing even though the field has been active for two decades up to now.
In the last decades, many neural network learning algorithms were proposed to extract PS []. These gradient-type algorithms could be claimed to be globally convergent.
In the class of MS tracking, many algorithms [].
1.1.3 Extension or Generalization of PCA
It can be found that the above-mentioned algorithms only focused on eigenvector extraction or eigen-subspace tracking with noncoupled rules. However, a serious speed stability problem exists in the most noncoupled rules [].
It is well known that the generalized eigen decomposition (GED) plays very important roles in various signal processing applications, e.g., data compression, feature extraction, denoising, antenna array processing, and classification. Though PCA, which is the special case of GED problem, has been widely studied, the adaptive algorithms for the GED problem are scarce. Fortunately, a few efficient online adaptive algorithms for the GED problem that can be applied in real-time applications have been proposed [].
Other extensions of PCA also include dual-purpose algorithm [.
1.2 Basis for Subspace Tracking
In Sect. , we have reviewed the PCA algorithm and its extensions and generalizations from the viewpoint of the feature extraction. In this section, from another viewpoint of subspace, we will discuss the concept of subspace and subspace tracking method.
1.2.1 Concept of Subspace
Definition 1
If
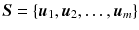
is the vector subset of vector space V , then the set W of all linear combinations of
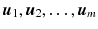











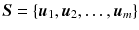 is the vector subset of vector space V , then the set W of all linear combinations of
is the vector subset of vector space V , then the set W of all linear combinations of