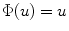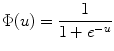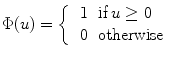Daniel S. Yeung , Ian Cloete , Daming Shi and Wing W. Y. Ng Natural Computing Series Sensitivity Analysis for Neural Networks 10.1007/978-3-642-02532-7_1 Springer-Verlag Berlin Heidelberg 2009
1. Introduction to Neural Networks
Abstract
The human brain consists of ten billion densely interconnected nerve cells, called neurons ; each connected to about 10,000 other neurons, with 60 trillion connections, synapses , between them. By using multiple neurons simultaneously, the brain can perform its functions much faster than the fastest computers in existence today. On the other hand, a neuron can be considered as a basic information-processing unit, whereas our brain can be considered as a highly complex, nonlinear and parallel biological information-processing network, in which information is stored and processed simultaneously. Learning is a fundamental and essential characteristic of biological neural networks. The ease with which they can learn led to attempts to emulate a biological neural network in a computer.
The human brain consists of ten billion densely interconnected nerve cells, called neurons ; each connected to about 10,000 other neurons, with 60 trillion connections, synapses , between them. By using multiple neurons simultaneously, the brain can perform its functions much faster than the fastest computers in existence today. On the other hand, a neuron can be considered as a basic information-processing unit, whereas our brain can be considered as a highly complex, nonlinear and parallel biological information-processing network, in which information is stored and processed simultaneously. Learning is a fundamental and essential characteristic of biological neural networks. The ease with which they can learn led to attempts to emulate a biological neural network in a computer.
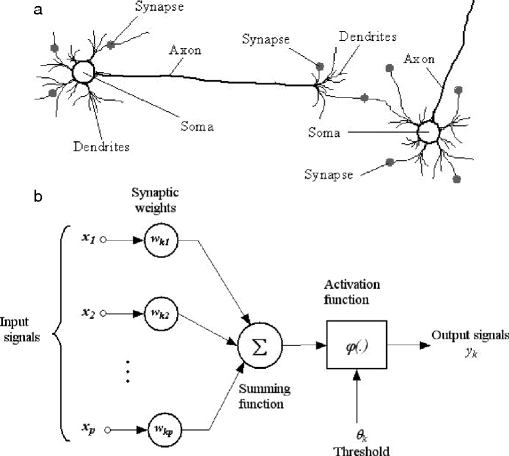
In the 1940s, McCulloch and Pitts proposed a model for biological neurons and biological neural networks. A stimulus is transmitted from dendrites to a soma via synapses, and axons transmit the response of one soma to another, as shown in Fig.. However, neural networks are far too simple to serve as realistic brain models on the cell level, but they might serve as very good models for the essential information processing tasks that organisms perform. This remains an open question because we have so little understanding of how the brain actually works (Gallant, 1993).
Fig. 1.1
Biological motivations of neural networks. (a) Neuroanatomy of living animals. (b) Connections of an artificial neuron
Table 1.1
Analogy between biological and artificial neurons
Biological Neurons | Artificial Neurons |
|---|
Soma | Sum + Activation Function |
Dendrite | Input |
Axon | Output |
Synapse | Weight |
In a neural network, neurons are joined by directed arcs connections . The neurons and arcs constitute the network topology . Each arc has a numerical weight that specifies the influence between two neurons. Positive weights indicate reinforcement; negative weights represent inhibition. The weights determine the behavior of the network, playing somewhat the same role as in a conventional computer program. Typically, there are many inputs for a single neuron, and a subsequent output of an activation function (or transfer function ). Some frequently used activation functions include:
Linear Function:
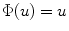
Log-Sigmoid Function:
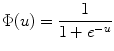
Hard Limit function:
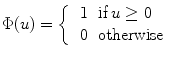
Rosenblatt (1958) devised the Perceptron, which is now widely used. Widrow and Hoff (1960) proposed the Adaline at the same time. The Perceptron and Adaline were the first practical networks and learning rules that demonstrated the high potential of neural networks.
Minsky and Papert (1969) criticized the Perceptron, because they found it is not powerful enough to do tasks such as parity and connectedness. As long as a neural network consists of a linear combiner followed by a nonlinear element , a single-layer Perceptron can perform pattern classification only on linearly separable patterns, regardless of the form of nonlinearity used. Minsky and Papert demonstrated the limitations of the Perceptron with the simplest XOR problem, and as a consequence the research in the field was suspended due to the lack of funding. Because of Minsky and Paperts conclusion, people lost confidence in neural networks. In the 1970s, the progress on neural networks continued at a much reduced pace, although some researchers, such as Amari, Anderson, Fukushima, Grossberg and Kohonen, kept working on it.
In 1985, Ackley, Hinton and Sejnowski described the Boltzmann machine, which is more powerful than a Perceptron, and demonstrated a successful application NETtalk.
Rumelhart, Hinton and Williams (1986) are recognized for their milestone work the Multilayer Perceptron (MLP) with backpropagation, which remained the dominant neural network architecture for more than ten years. A sufficiently big MLP has been proven to be able to learn any function, and many variants of MLP have been proposed since then. In 1988, Radial Basis Functions (RBFs), introduced as an alternative to MLPs, speeded up MLP training (fast-prop).
From the 1990s to date, more and more research has been done to improve neural networks. The research agenda includes regularizers, probabilistic (Bayesian) inference, structural risk minimization and incorporation with evolutionary computation.
1.1 Properties of Neural Networks
Neural networks can be described according to their network, cell, dynamic , and learning properties as follows:
Network Properties. A neural network is an architecture consisting of many neurons, which work together to respond to the inputs. We sometimes consider a network as a black-box function. Here the external world presents inputs to the input cells and receives network outputs from the output cells. Intermediate cells are not seen externally, and for this reason they are often called hidden units . We classify networks as either feedforward networks if they do not contain directed cycles or recurrent networks if they do contain such cycles. It is often convenient to organize the cells of a network into layers.