Stochastic Calculus for Quantitative Finance
Alexander A. Gushchin

Copyright
First published 2015 in Great Britain and the United States by ISTE Press Ltd and Elsevier Ltd Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address: ISTE Press Ltd 27-37 St Georges Road London SW19 4EU UK www.iste.co.uk Elsevier Ltd The Boulevard, Langford Lane Kidlington, Oxford, OX5 1GB UK www.elsevier.com
Notices Knowledge and best practice in this field are constantly changing. As new research and experience broaden our understanding, changes in research methods, professional practices, or medical treatment may become necessary. Practitioners and researchers must always rely on their own experience and knowledge in evaluating and using any information, methods, compounds, or experiments described herein. In using such information or methods they should be mindful of their own safety and the safety of others, including parties for whom they have a professional responsibility.
To the fullest extent of the law, neither the Publisher nor the authors, contributors, or editors, assume any liability for any injury and/or damage to persons or property as a matter of products liability, negligence or otherwise, or from any use or operation of any methods, products, instructions, or ideas contained in the material herein. For information on all our publications visit our website at http://store.elsevier.com/ ISTE Press Ltd 2015 The rights of Alexander A. Gushchin to be identified as the author of this work have been asserted by him in accordance with the Copyright, Designs and Patents Act 1988. British Library Cataloguing-in-Publication Data A CIP record for this book is available from the British Library Library of Congress Cataloging in Publication Data A catalog record for this book is available from the Library of Congress ISBN 978-1-78548-034-8 Printed and bound in the UK and US
Basic Notation
The symbol

indicates the end of the proof. The symbol := means put by definition. R=(,+)
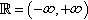
= the set of real numbers, R+=[0,+)
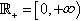
.
Rd 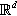 = d -dimensional Euclidean space. Q
= d -dimensional Euclidean space. Q 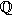 = the set of rational numbers, Q+=QR+
= the set of rational numbers, Q+=QR+ 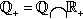 . N={1,2,3,}
. N={1,2,3,} 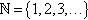 = the set of natural numbers. a b = max{ a , b }, a b = min{ a , b } for a,bR
= the set of natural numbers. a b = max{ a , b }, a b = min{ a , b } for a,bR 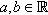 . a + = a 0, a = ( a ) 0 for aR
. a + = a 0, a = ( a ) 0 for aR 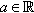 . 1B
. 1B 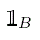 = the indicator function of the set B . 1B
= the indicator function of the set B . 1B 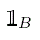 = the indicator function of the set B .
= the indicator function of the set B .
E = expectation. E(|G) 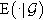 = conditional expectation with respect to the -algebrs G
= conditional expectation with respect to the -algebrs G 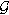 . FG=(FG)
. FG=(FG) 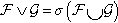 = the smallest -algebra containing the -algebras F
= the smallest -algebra containing the -algebras F 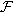 and G
and G 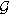 . AF=(AF)
. AF=(AF) 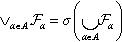 = the smallest -algebra containing the -algebras F
= the smallest -algebra containing the -algebras F 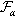 , A .
, A .
Preface
The arbitrage theory for general models of financial markets in continuous time is based on the heavy use of the theory of martingales and stochastic integration (see the monograph by Delbaen and Schchermayer []. The last section is devoted to a-martingales and the AnselStricker theorem.
Some results are given without proofs. These include the section theorem, classical Doobs theorems on martingales, the BurkholderDavisGundy inequality and Its formula. Our method of presentation may be considered as old-fashioned, compared to, for example, the monograph by Protter [], which begins with an introduction of the notion of a semimartingale; in our book, semimartingales appear only in the final chapter. However, the authors experience based on the graduate courses taught at the Department of Mechanics and Mathematics of Moscow State University, indicates that our approach has some advantages. The text is intended for a reader with a knowledge of measure-theoretic probability and discrete-time martingales. Some information on less standard topics (theorems on monotone classes, uniform integrability, conditional expectation for nonintegrable random variables and functions of bounded variation) can be found in the Appendix.
The basic idea, which the author pursued when writing this book, was to provide an affordable and detailed presentation of the foundations of the theory of stochastic integration, which the reader needs to know before reading more advanced literature on the subject, such as Jacod []. The text is accompanied by more than a hundred exercises. Almost all of them are simple or are supplied with hints. Many exercises extend the text and are used later. The work on this book was partially supported by the International Laboratory of Quantitative Finance, National Research University Higher School of Economics and Russian Federation Government (grant no. 14.A12.31.0007).
I wish to express my sincere thanks to Tatiana Belkina for a significant and invaluable assistance in preparing the manuscript. Alexander Gushchin, Moscow, May 2015
List of Statements
D efinitions
| Definition 1.1 |
| Definition 1.2 |
| Definition 1.3 |














 indicates the end of the proof. The symbol := means put by definition. R=(,+)
indicates the end of the proof. The symbol := means put by definition. R=(,+) 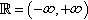 = the set of real numbers, R+=[0,+)
= the set of real numbers, R+=[0,+) 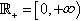 .
. 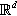 = d -dimensional Euclidean space. Q
= d -dimensional Euclidean space. Q 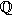 = the set of rational numbers, Q+=QR+
= the set of rational numbers, Q+=QR+ 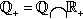 . N={1,2,3,}
. N={1,2,3,} 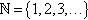 = the set of natural numbers. a b = max{ a , b }, a b = min{ a , b } for a,bR
= the set of natural numbers. a b = max{ a , b }, a b = min{ a , b } for a,bR 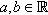 . a + = a 0, a = ( a ) 0 for aR
. a + = a 0, a = ( a ) 0 for aR 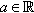 . 1B
. 1B 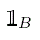 = the indicator function of the set B . 1B
= the indicator function of the set B . 1B 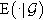 = conditional expectation with respect to the -algebrs G
= conditional expectation with respect to the -algebrs G 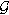 . FG=(FG)
. FG=(FG) 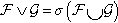 = the smallest -algebra containing the -algebras F
= the smallest -algebra containing the -algebras F 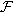 and G
and G 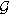 . AF=(AF)
. AF=(AF) 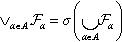 = the smallest -algebra containing the -algebras F
= the smallest -algebra containing the -algebras F  , A .
, A .