Ferrari Patrik L. - Reflected Brownian Motions in the KPZ Universality Class

The Author(s) 2017

Thomas Weiss 1, Patrik Ferrari 2 and Herbert Spohn 3

Back in 1931 Hans Bethe diagonalized the hamiltonian of the one-dimensional Heisenberg spin chain through what is now called the Bethe ansatz (Bethe ).

On a mathematical level, quantum hamiltonians and generators of Markov processes have a comparable structure. Thus one could imagine that the Bethe ansatz is equally useful for interacting stochastic systems with many particles. The first indication came somewhat indirectly from the Kardar-Parisi-Zhang equation (Kardar et al. ). The KPZ equation is a stochastic PDE governing the time-evolution of a height function h ( x , t ) at spatial point x and time t , , , . 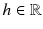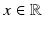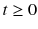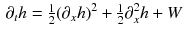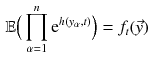The equation reads 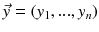with W ( x , t ) normalized space-time white noise. We use here units of height, space, and time such that all coupling parameters take a definite value. For a solution of ( ). More precisely, one defines with . Then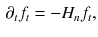 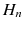where is the n -particle Lieb-Liniger hamiltonian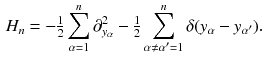 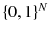Almost thirty years later the generator of the asymmetric simple exclusion process (ASEP) was diagonalized through the Bethe ansatz. In case of N sites, the ASEP configuration space is signalling a similarity with quantum spin chains. In fact, the ASEP generator can be viewed as the Heisenberg chain with an imaginary XY-coupling. For the totally asymmetric limit (TASEP) and half filled lattice, Gwa and Spohn () established that the spectral gap of the generator is of order 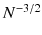. The same order is argued for the KPZ equation. This led to the strong belief that, despite their very different set-up, both models have the same statistical properties on large space-time scales. In the usual jargon of statistical mechanics, both models are expected to belong to the same universality class, baptized KPZ universality class according to its most prominent representative.

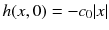The KPZ equation is solved with particular initial conditions. Of interest are (i) sharp wedge , in the limit 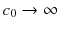, (ii) flat , 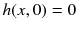, and (iii) stationary , 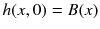with B ( x ) two sided Brownian motion. The quantity of prime interest is the distribution of h (0, t ) for large t . More ambitiously, but still feasible in some models, is the large time limit of the joint distribution of .

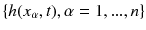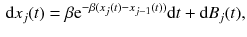
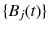In our notes we consider an integrable system of interacting diffusions, which is governed by the coupled stochastic differential equations where a collection of independent standard Brownian motions. For the parameter 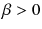we will eventually consider only the limit 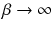. But for the purpose of our discussion we keep 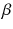finite for a while. In fact there is no choice, no other system of this structure is known to be integrable. The index set depends on the problem, mostly we choose 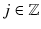. Note that 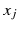interacts only with its left index neighbor 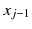. The drift depends on the slope, as it should be for a proper height function. But the exponential dependence on 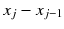is very special, however familiar from other integrable systems. The famous Toda chain (Toda ).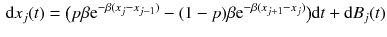

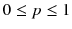Interaction with only the left neighbor corresponds to the total asymmetric version. Partial asymmetry would read with . These are non-reversible diffusion processes. Only in the symmetric case, 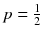, the drift is the gradient of a potential and the diffusion process is reversible. Then the model is no longer in the KPZ universality class and has very distinct large scale properties, see Guo et al. (), for example.