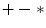1. Extreme Accuracy in Symbolic Regression
Abstract
Although recent advances in symbolic regression (SR) have promoted the field into the early stages of commercial exploitation, the poor accuracy of SR is still plaguing even the most advanced commercial packages today. Users expect to have the correct formula returned, especially in cases with zero noise and only one basis function with minimally complex grammar depth. Poor accuracy is a hindrance to greater academic and industrial acceptance of SR tools.
In a previous paper, the poor accuracy of Symbolic Regression was explored, and several classes of test formulas, which prove intractable for SR, were examined. An understanding of why these test problems prove intractable was developed. In another paper a baseline Symbolic Regression algorithm was developed with specific techniques for optimizing embedded real numbers constants. These previous steps have placed us in a position to make an attempt at vanquishing the SR accuracy problem.
In this chapter we develop a complex algorithm for modern symbolic regression which is extremely accurate for a large class of Symbolic Regression problems. The class of problems, on which SR is extremely accurate, is described in detail. A definition of extreme accuracy is provided, and an informal argument of extreme SR accuracy is outlined in this chapter. Given the critical importance of accuracy in SR, it is our suspicion that in the future all commercial Symbolic Regression packages will use this algorithm or a substitute for this algorithm.
Introduction
The discipline of Symbolic Regression (SR) has matured significantly in the last few years. There is at least one commercial package on the market for several years ( ).
Yet, despite the increasing sophistication of commercial SR packages, there have been serious issues with SR accuracy even on simple problems (Korns ). Clearly the perception of SR as a must use tool for important problems or as an interesting heurism for shedding light on some problems, will be greatly affected by the demonstrable accuracy of available SR algorithms and tools. The depth and breadth of SR adoption in industry and academia will be greatest if a very high level of accuracy can be demonstrated for SR algorithms.
In Korns ().
In this chapter we enhance the previous baseline with a complex multi-island algorithm for modern symbolic regression which is extremely accurate for a large class of Symbolic Regression problems. The class of problems, on which SR is extremely accurate, is described in detail. A definition of extreme accuracy is provided, and an informal argument of extreme SR accuracy is outlined in this chapter.
Before continuing with the details of our extreme accuracy algorithm, we proceed with a basic introduction to general nonlinear regression. Nonlinear regression is the mathematical problem which Symbolic Regression aspires to solve. The canonical generalization of nonlinear regression is the class of Generalized Linear Models (GLMs) as described in Nelder and Wedderburn (). A GLM is a linear combination of I basis functions B i ; i=0,1, I, a dependent variable y, and an independent data point with M features x=0, x1, x2, , x M 1>: such that
As a broad generalization, GLMs can represent any possible nonlinear formula. However the format of the GLM makes it amenable to existing linear regression theory and tools since the GLM model is linear on each of the basis functions B i . For a given vector of dependent variables, Y, and a vector of independent data points, X, symbolic regression will search for a set of basis functions and coefficients which minimize err . In Koza () the basis functions selected by symbolic regression will be formulas as in the following examples:
If we are minimizing the normalized least squared error, NLSE (Korns ) the genome and the individual are the same Lisp s-expression which is usually illustrated as a tree. Of course the tree-view of an s-expression is a visual aid, since a Lisp s-expression is normally a list which is a special Lisp data structure. Without altering or restricting basic tree-based GP in any way, we can view the individuals not as trees but instead as s-expressions such as this depth 2 binary tree s-exp: (/ (+ x 2 3.45) ( x 0 x 2 )) , or this depth 2 irregular tree s-exp: (/ (+ x 4 3.45) 2.0) .
In basic GP, applied to symbolic regression, the non-terminal nodes are all operators (implemented as Lisp function calls), and the terminal nodes are always either real number constants or features. The maximum depth of a GP individual is limited by the available computational resources; but, it is standard practice to limit the maximum depth of a GP individual to some manageable limit at the start of a symbolic regression run.
Given any selected maximum depth k, it is an easy process to construct a maximal binary tree s-expression U k , which can be produced by the GP system without violating the selected maximum depth limit. As long as we are reminded that each f represents a function node while each t represents a terminal node, the construction algorithm is simple and recursive as follows.
The basic GP symbolic regression system (Koza ) contains a set of functions F, and a set of terminals T. If we let tT, and fF
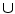
, where (a, b) = (a) =a , then any basis function produced by the basic GP system will be represented by at least one element of U k . Adding the function allows U k to express all possible basis functions generated by the basic GP system to a depth of k . Note to the reader , the function performs the job of a pass-through function. The function allows a fixed-maximal-depth expression in U k to express trees of varying depth, such as might be produced from a GP system. For instance, the varying depth GP expression x 2 +(x 3 x 5 ) = (x 2 , 0.0)+(x 3 x 5 ) = + ((x 2 , 0.0) (x 3 x 5 )) which is a fixed-maximal-depth expression in U2.
In addition to the special pass through function , in our system we also make additional slight alterations to improve coverage, reduce unwanted errors, and restrict results from wandering into the complex number range. All unary functions, such as cos , are extended to ignore any extra arguments so that, for all unary functions, cos(a,b) =cos(a) . The sqroot and ln functions are extended for negative arguments so that sqroot(a) =sqroot(abs(a)) and ln(a) =ln(abs(a)) .
Given this formalism of the search space, it is easy to compute the size of the search space, and it is easy to see that the search space is huge even for rather simple basis functions. For our use in this chapter the function set will be the following functions: F= (
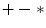











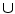 , where (a, b) = (a) =a , then any basis function produced by the basic GP system will be represented by at least one element of U k . Adding the function allows U k to express all possible basis functions generated by the basic GP system to a depth of k . Note to the reader , the function performs the job of a pass-through function. The function allows a fixed-maximal-depth expression in U k to express trees of varying depth, such as might be produced from a GP system. For instance, the varying depth GP expression x 2 +(x 3 x 5 ) = (x 2 , 0.0)+(x 3 x 5 ) = + ((x 2 , 0.0) (x 3 x 5 )) which is a fixed-maximal-depth expression in U2.
, where (a, b) = (a) =a , then any basis function produced by the basic GP system will be represented by at least one element of U k . Adding the function allows U k to express all possible basis functions generated by the basic GP system to a depth of k . Note to the reader , the function performs the job of a pass-through function. The function allows a fixed-maximal-depth expression in U k to express trees of varying depth, such as might be produced from a GP system. For instance, the varying depth GP expression x 2 +(x 3 x 5 ) = (x 2 , 0.0)+(x 3 x 5 ) = + ((x 2 , 0.0) (x 3 x 5 )) which is a fixed-maximal-depth expression in U2.