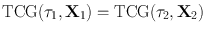This textbook deals with astronomical (geodetic) reference systems. These present special kinds of spatial-temporal reference systems that play a fundamental role, especially in the vicinity of the Earth.
The phrase reference system implies more than a mere mathematical coordinate system in a spacetime manifold: it points towards a labeling of spacetime events in the near Earth space that has to be achieved with dedicated observing and analysis systems. Such events are supposed to have a small extent in space (here) and time (now). Examples are the phase centers in GPS or radio antennas, or the center of mass of a planet at a certain instant of time.
1.1.1 The Problem of Time
What is time? If no one ask of me, I know; if I wish to explain to him who asks, I know not.
This sentence by St. Augustine starkly illuminates the difficulties related with an analysis of the notion of time (or any other fundamental scientific notion like space, matter, life, etc.). Here we would like to focus only on two aspects of the notion of time. The first is of a theoretical, the second more of a practical, nature. On the theoretical side, Newton confronted the relative, apparent, and common time of ordinary life with an absolute, true, and mathematical time that by itself and due to its own nature flows steadily without respect to some material object. This theoretical concept later was overthrown by Einsteins theory of gravity, due to conflicts with practical aspects.
The practical aspects are related simply to how time is measured. The famous Nobel Prize winner Richard Feynman once said: not what time is of interest in physics, but how it is measured. In this sense, the conceptual aspect of time is related with the art of clockmaking. Any clock uses a physical process whose laws are known and whose progression can be indicated. In practice, periodic processes are used exclusively, i.e., time measurement usually is a frequency determination.
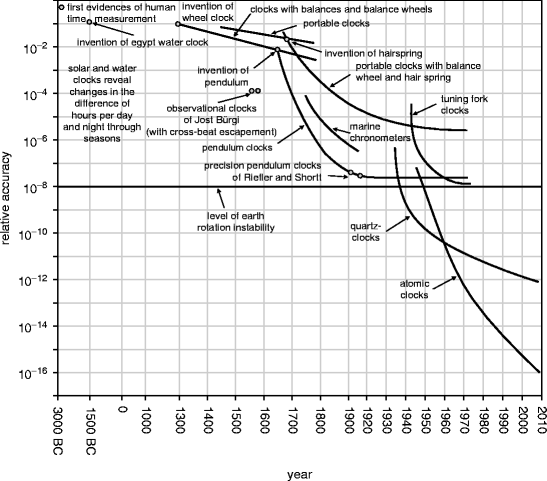
Figure provides an overview over the art of clock making from 3000 BC till now. One sees that the accuracy of clocks during that period of time increased by about fourteen orders of magnitude.
Fig. 1.1
The art of clockmaking over the course of time
The sundial dates back to the Egyptian period, around 1500 BC . A stick or pillar was fixed to the ground, and from its shadow time was deduced. Water clocks were in use by the Egyptians, Romans, and Chinese. Significant progress in accuracy was achieved by the introduction of the pendulum as an oscillator by Galileo Galilei some time around 1600 and realized by Christian Huygens in 1656. The seafarers longitude problem is well known: determining a ships latitude by astronomical means was straightforward, but not the longitude. One way to determine geographic longitude at sea is by means of a marine chronometer that carries the time at a given port and can be compared with local time as determined by astronomical observations. However, for a loss or gain of only a minute per day, we end up with an error of half an hour for a sea passage of 1 month. As during 30min the Earth revolves by an angle of 7.5, this corresponds to a navigational error of several hundred miles.
At the beginning of the eighteenth century, a Board of Longitude appointed by the British parliament initiated a scientific competition to find a practical method of solving the longitude problem (Sobel and Andrewes, ), stands comparison with a modern mechanical clock. The spring systems produced an almost constant drive even during winding, and inaccuracies caused by temperature changes during the sea trip were practically eliminated by a regulator controlled by a bimetallic strip. In the official test, the clock was three times as precise as the commission had requested: after a passage of 22 days from Portsmouth to Barbados, the referees compared the readings from the marine chronometer with the orbits of Jupiters Galilean moons. The error was found to be less than 39s! This implies that the relative accuracy of Harrisons H4 was about 1.8s in a day or a relative accuracy of 2 105.
Fig. 1.2
John Harrisons marine chronomtere. Courtesy of the National Maritime Museum, Greenwich, London
At the beginning of the twentieth century, the accuracy of marine chronometers was about a tenth of a second per day; pendulum clocks were built with an accuracy of better than a hundredth of a second per day. A huge advance in the accuracy of clocks was achieved by employing oscillations of certain crystals instead of pendulum or hairspring. Even more accurate are modern atomic clocks, like cesium clocks, rubidium clocks, or hydrogen maser clocks. A new version of such classical atomic clocks in form of fountain clocks became popular in recent decades. Such classical atomic clocks are based upon atomic transition frequencies that lie in the microwave region; due to their stochastic character, one needs to average times over minutes and days to achieve the highest accuracies and stabilities. Meanwhile, new kinds of atomic clocks have been developed that use atomic transitions with much higher frequencies, i.e., optical clocks, for which averaging times are significantly shorter. Clock stabilities (accuracies) are now approaching 1017, a number that should be compared with the age of the universe of about 4 1017s.
Now, according to relativity, the time indicated by a particular clock depends upon the clocks velocity with respect to the observer who tries to read the clock and also upon the gravitational potential that prevails at the clocks position. The readout of a certain clock for some co-moving observer (the clocks proper time) is not a good tool for other observers. For that reason, the introduction of standardized timescales is of great importance for practical applications. The readings of atomic clocks are the basis for all astronomical timescales now in use (note that some times, notably universal time and sidereal time, are in fact angles that describe Earth rotation and are not timescales in the strict sense). A timescale is a carefully selected time coordinate that can be used for any event that occurs in a certain spatial region such as the vicinity of the Earth; it should have a simple and well-defined relation to the proper time of a real clock in that spatial region.
Due to relativity, one has in particular to distinguish geocentric from barycentric (the barycenter of the solar system) timescales. The basic geocentric timescale is geocentric coordinate time (TCG). TCG is the time coordinate of the geocentric celestial reference system (GCRS). Its practical realization is achieved through certain formulae that relate the proper times of atomic clocks and their spatial GCRS coordinates X to TCG. TCG is an important tool for the synchronization of clocks: two clocks showing proper time 1 and 2 are called synchronous if their corresponding TCG values agree, i.e., if