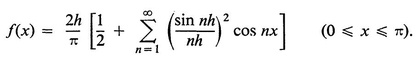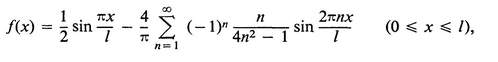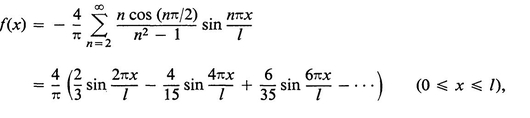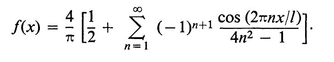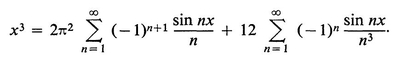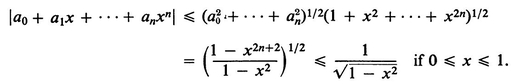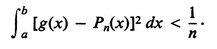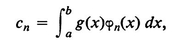Silverman Richard A. - Fourier Series

Bochner, S., Lectures on Fourier Integrals, translated by M. Tenenbaum and H. Pollard, Princeton University Press, Princeton (1959).

Bochner, S. and K. Chandrasekharan, Fourier Transforms, Princeton University Press, Princeton (1949).

Byerly, W. A., An Elementary Treatise on Fouriers Series and Spherical, Cylindrical, and Ellipsoidal Harmonics, Ginn and Co., Boston (1893).

Carslaw, H. S., Introduction to the Theory of Fouriers Series and Integral, Macmillan & Co., Ltd., London (1930), reprinted by Dover Publications, Inc., New York.

Carslaw, H. S. and J. C. Jaeger, Conduction of Heat in Solids, second edition, Oxford University Press, New York (1959).

Churchill, R. V., Fourier Series and Boundary Value Problems, McGraw-Hill Book Co., Inc., New York (1941).

Franklin, P., Fourier Methods, McGraw-Hill Book Co., Inc., New York (1949), reprinted by Dover Publications, Inc., New York.

Goldberg, R. R., Fourier Transforms, Cambridge University Press, New York (1961).

Jackson, D., Fourier Series and Orthogonal Polynomials, Carus Mathematical Monograph No. 6, Math. Assoc. America (1941).

Jeffrey, R. L., Trigonometric Series, University of Toronto Press, Toronto (1956).

McLachlan, N. W., Bessel Functions For Engineers, second edition, Oxford University Press, New York (1955).

Rogosinski, W. W., Fourier Series, translated by H. Cohn and F. Steinhardt, second edition, Chelsea Publishing Co., New York (1959).

Sneddon, I. A., Fourier Transforms, McGraw-Hill Book Co., Inc., New York (1951).

Titchmarsh, E. C., Introduction to the Theory of Fourier Integrals, second edition, Oxford University Press, New York (1948).

Titchmarsh, E. C., Eigenfunction Expansions Associated with Second Order Dufferential Equations, Oxford University Press, New York, Part I (1946), Part II (1958).

Watson, G. N., A Treatise on the Theory of Bessel Functions, second edition, Cambridge University Press, New York (1945).

Wiener, N., The Fourier Integral and Certain of Its Applications, Cambridge University Press, New York (1933), reprinted by Dover Publications, Inc., New York. sity Press, New York (1933), reprinted by Dover Publications, Inc., New York.

Zygmund, A., Trigonometric Series, in two volumes, Cambridge University Press, New York (1959).

ANSWERS TO PROBLEMS

CHAPTER 1

• 1. 
  2. 
  3. 
  4. 
• 1. 
  2. 
• 1. 

     (What happens when a is an integer?)

  2. 

     except for the value x = , where the sum equals 1/2. (Why?)

  3. 
• 1. 
     except for the value x = //2, where the sum equals 1/2;
  2. 

     except for the value x = //2, where the sum equals 0.

• .
  
• .
  

  Hence

  

  so that

  
• .
  1. 
  2. 

CHAPTER 2

3. By the Cauchy inequality

Now integrate. The sharper estimate is obtained by direct use of the Schwarz inequality.

Use the Schwarz inequality with one function equal to |1 + e in x + + e in k x| | and the other equal to 1.

Use the Schwarz inequality.

Suppose g(x) is orthogonal to all the i (x), and let P n (x) = a n (x) + + a n n (x) be such that

Then || g ||2 + ||P n ||2 < 1/ n , so that || g ||2 = 0, i.e., g( x) 0, since g( x ) is continuous.

1. No orthogonal function exists, since if g were such a function and if
   
   then 0 = c + c = c0 + c2 = C0 + C3 = , i.e., c = c = c = , which violates Bessels inequality (Sec. 6) unless all the ci are zero; b) No orthogonal function exists, by a similar proof; c) An orthogonal function g exists. In fact, consider the continuous function
   

1. If g = a 00 + + a n n is zero, then

   0 = || g ||2 = | a 0|2(0, 0) + + |a n | ( n n ),

   i.e., a 0 = a = = a n = 0 [for the definition of (, ), see Prob. 10 and Ch. 2, Sec. 10]; b) A polynomial of degree n has at most n real zeros, unless it vanishes identically.

Use repeated integration by parts.

1. 
2.