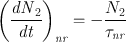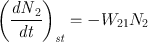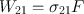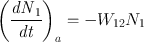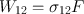In this introductory chapter, the fundamental processes and the main ideas behind laser operation are introduced in a very simple way. The properties of laser beams are also briefly discussed. The main purpose of this chapter is thus to introduce the reader to many of the concepts that will be discussed later on, in the book, and therefore help the reader to appreciate the logical organization of the book.
1.1 Spontaneous and Stimulated Emission, Absorption
To describe the phenomenon of spontaneous emission, let us consider two energy levels, 1 and 2, of some atom or molecule of a given material, their energies being E 1 and E 2 ( E 1 < E 2) (Fig. a). As far as the following discussion is concerned, the two levels could be any two out of the infinite set of levels possessed by the atom. It is convenient, however, to take level 1 to be the ground level. Let us now assume that the atom is initially in level 2. Since E 2 > E 1, the atom will tend to decay to level 1. The corresponding energy difference, E 2 E 1, must therefore be released by the atom. When this energy is delivered in the form of an electromagnetic (e.m. from now on) wave, the process will be called spontaneous (or radiative ) emission . The frequency 0 of the radiated wave is then given by the well known expression
where h is Plancks constant. Spontaneous emission is therefore characterized by the emission of a photon of energy
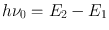
, when the atom decays from level 2 to level 1 (Fig. a). Note that radiative emission is just one of the two possible ways for the atom to decay. The decay can also occur in a nonradiative way. In this case the energy difference E 2 E 1 is delivered in some form of energy other than e.m. radiation (e.g. it may go into kinetic or internal energy of the surrounding atoms or molecules). This phenomenon is called non-radiative decay .
Fig. 1.1
Schematic illustration of the three processes: (a) spontaneous emission; (b) stimulated emission; (c) absorption.
Let us now suppose that the atom is found initially in level 2 and that an e.m. wave of frequency = o (i.e., equal to that of the spontaneously emitted wave) is incident on the material (Fig. b). Since this wave has the same frequency as the atomic frequency, there is a finite probability that this wave will force the atom to undergo the transition 2 1. In this case the energy difference E 2 E 1 is delivered in the form of an e.m. wave that adds to the incident one. This is the phenomenon of stimulated emission . There is a fundamental difference between the spontaneous and stimulated emission processes. In the case of spontaneous emission, the atoms emits an e.m. wave that has no definite phase relation with that emitted by another atom. Furthermore, the wave can be emitted in any direction. In the case of stimulated emission, since the process is forced by the incident e.m. wave, the emission of any atom adds in phase to that of the incoming wave and along the same direction.
Let us now assume that the atom is initially lying in level 1 (Fig. c). If this is the ground level, the atom will remain in this level unless some external stimulus is applied to it. We shall assume, then, that an e.m. wave of frequency = o is incident on the material. In this case there is a finite probability that the atom will be raised to level 2. The energy difference E 2 E 1 required by the atom to undergo the transition is obtained from the energy of the incident e.m. wave. This is the absorption process.
To introduce the probabilities for these emission and absorption phenomena, let N be the number of atoms (or molecules) per unit volume which, at time t , are lying in a given energy level. From now on the quantity N will be called the population of the level.
For the case of spontaneous emission, the probability for the process to occur can be defined by stating that the rate of decay of the upper state population, ( dN 2 dt ) sp , must be proportional to the population N 2. We can therefore write
where the minus sign accounts for the fact that the time derivative is negative. The coefficient A , introduced in this way, is a positive constant and is called the rate of spontaneous emission or the Einstein A coefficient (an expression for A was in fact first obtained by Einstein from thermodynamic considerations). The quantity
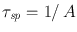
is called the spontaneous emission (or radiative) lifetime. Similarly, for non-radiative decay, we can often write
where nr is referred to as the non-radiative decay lifetime. Note that, for spontaneous emission, the numerical value of A (and sp ) depends only on the particular transition considered. For non-radiative decay, nr depends not only on the transition but also on the characteristics of the surrounding medium.
We can now proceed, in a similar way, for the stimulated processes (emission or absorption). For stimulated emission we can write
where ( dN 2 dt ) st is the rate at which transitions 2 1 occur as a result of stimulated emission and W 21 is called the rate of stimulated emission. Just as in the case of the A coefficient defined by Eq. () the coefficient W 21 also has the dimension of (time ) 1. Unlike A , however, W 21 depends not only on the particular transition but also on the intensity of the incident e.m. wave. More precisely, for a plane wave, it will be shown that we can write
where F is the photon flux of the wave and 21 is a quantity having the dimension of an area (the stimulated emission cross section ) and depending on the characteristics of the given transition.
In a similar fashion to Eq. (), we can define an absorption rate W 21 by means of the equation
where ( dN 1 dt ) a is the rate of the 1 2 transitions due to absorption and N 1 is the population of level 1. Furthermore, just as in Eq. (), we can write
where 12 is some characteristic area (the absorption cross section ), which depends only on the particular transition.
In what has just been said, the stimulated processes have been characterized by the stimulated emission and absorption cross-sections, 21 and 12, respectively. Now, it was shown by Einstein at the beginning of the twentieth century that, if the two levels are non-degenerate, one always has W 21 = W 12 and 21 = 12. If levels 1 and 2 are g 1-fold and g 2-fold degenerate, respectively one has instead
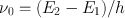
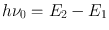 , when the atom decays from level 2 to level 1 (Fig. a). Note that radiative emission is just one of the two possible ways for the atom to decay. The decay can also occur in a nonradiative way. In this case the energy difference E 2 E 1 is delivered in some form of energy other than e.m. radiation (e.g. it may go into kinetic or internal energy of the surrounding atoms or molecules). This phenomenon is called non-radiative decay .
, when the atom decays from level 2 to level 1 (Fig. a). Note that radiative emission is just one of the two possible ways for the atom to decay. The decay can also occur in a nonradiative way. In this case the energy difference E 2 E 1 is delivered in some form of energy other than e.m. radiation (e.g. it may go into kinetic or internal energy of the surrounding atoms or molecules). This phenomenon is called non-radiative decay . 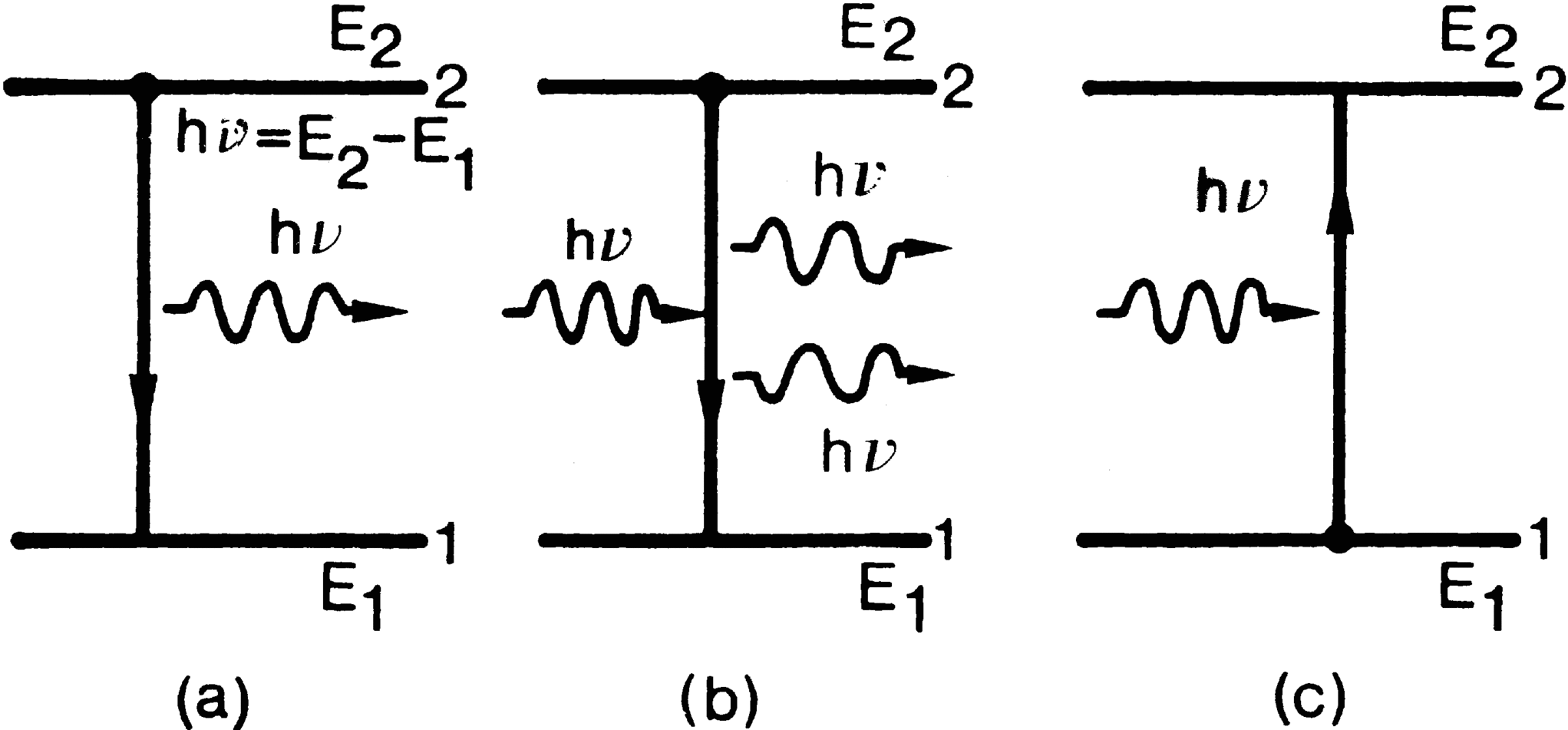
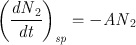
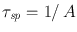 is called the spontaneous emission (or radiative) lifetime. Similarly, for non-radiative decay, we can often write
is called the spontaneous emission (or radiative) lifetime. Similarly, for non-radiative decay, we can often write