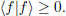CONTENTS

 Published by
Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224
USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601
UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE
British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library.
PROBLEMS AND SOLUTIONS IN QUANTUM COMPUTING AND QUANTUM INFORMATION
4th Edition Copyright 2018 by World Scientific Publishing Co. Ltd.
All rights reserved. All rights reserved.
This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the publisher. For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher. ISBN 978-981-3238-40-4 ISBN 978-981-3239-28-9 (pbk) For any available supplementary material, please visit http://www.worldscientific.com/worldscibooks/10.1142/10943#t=suppl Printed in Singapore
Preface
The purpose of this book is to supply a collection of problems in quantum computing and quantum information together with their detailed solutions which will prove to be valuable to graduate students as well as to research workers in these fields. All the important concepts and topics such as quantum gates and quantum circuits, quantum channels, entanglement, teleportation, Bell states, Bell inequality, Schmidt decomposition, quantum Fourier transform, magic gate, von Neumann entropy, quantum channels, quantum cryptography, quantum error correction, coherent states, coherent Bell states, squeezed states, POVM measurement, beam splitter, homodyne detection and Kerr Hamilton operator are included. The topics range in difficulty from elementary to advanced. Almost all problems are solved in detail and most of the problems are self-contained.
All relevant definitions are given. Students can learn important principles and strategies required for problem solving. Teachers will also find this text useful as a supplement, since important concepts and techniques are developed in the problems. The book can also be used as a text or a supplement for linear and multilinear algebra or matrix theory. Each chapter also includes supplementary problems. Most chapters also include programming problems in Maxima and SymbolicC++.
The material was tested in our lectures given around the world. Any useful suggestions and comments are welcome. The International School for Scientific Computing (ISSC) provides certificate courses for this subject. Please contact the first author if you want to do this course. More quantum computing exercises can be found on the web page given below. , |n 1}
The
Pauli spin matricesare used extensively in the book. , |
n1}The
Pauli spin matricesare used extensively in the book.
They are given by 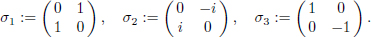 The spin-
The spin- matrix S1, S2, S3 are given by S1 =
matrix S1, S2, S3 are given by S1 =  1, S2 =
1, S2 =  2, S3 =
2, S3 =  3. The Dirac gamma matrices are given by
3. The Dirac gamma matrices are given by 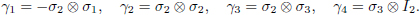 The concept of a Hilbert space will be used throughout the book. A Hilbert space is a set, H of elements, or vectors, (f, g, h,...) which satisfies the following conditions (1) -- (5). (1) If f and g belong to H , then there is a unique element of H , denoted by f + g, the operation of addition (+) being invertible, commutative and associative. (2) If c is a complex number, then for any f in H , there is an element cf of H ; and the multiplication of vectors by complex numbers thereby defined satisfies the distributive conditions
The concept of a Hilbert space will be used throughout the book. A Hilbert space is a set, H of elements, or vectors, (f, g, h,...) which satisfies the following conditions (1) -- (5). (1) If f and g belong to H , then there is a unique element of H , denoted by f + g, the operation of addition (+) being invertible, commutative and associative. (2) If c is a complex number, then for any f in H , there is an element cf of H ; and the multiplication of vectors by complex numbers thereby defined satisfies the distributive conditions  (3) Hilbert spaces H possess a zero element, 0, characterized by the property that 0 + f = f for all vectors f in H . (4) For each pair of vectors f, g in H , there is a complex number f|g, termed the inner product or scalar product, of f with g, such that
(3) Hilbert spaces H possess a zero element, 0, characterized by the property that 0 + f = f for all vectors f in H . (4) For each pair of vectors f, g in H , there is a complex number f|g, termed the inner product or scalar product, of f with g, such that 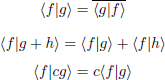 and
and 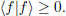
| garbitrary orthonormal basis for C n |
| |+, |, |+, | | Bell states in C 4 |
| h/2 with h the Planck constant |
| t | time |
| frequency |
| k | wave vector |
| r | space coordinates |
| p | momentum |
| b, b | Bose annihilation and creation operators |
| |n | number states, Fock states n = 0, 1, 2,... |
| | | coherent state, C |
| | | squeezed state, C |
| D() | displacement operator, C |
| S() | one-mode squeezing operator, C |
| s | squeezing parameter |
| c, c | Fermi annihilation and creation operators |
| E | electric field |
| B | magnetic induction |
| P | electric polarization |
| garbitrary orthonormal basis for C n |
| |+, |, |+, | | Bell states in C 4 |
| h/2 with h the Planck constant |
| t | time |
| frequency |
| k | wave vector |
| r | space coordinates |
| p | momentum |
| b, b | Bose annihilation and creation operators |
| |n | number states, Fock states n = 0, 1, 2,... |
| | | coherent state, C |
| | | squeezed state, C |
| D() | displacement operator, C |
| S() | one-mode squeezing operator, C |
| s | squeezing parameter |
| c, c | Fermi annihilation and creation operators |
| E | electric field |
| B | magnetic induction |
| P | electric polarization |
Next page













 Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. PROBLEMS AND SOLUTIONS IN QUANTUM COMPUTING AND QUANTUM INFORMATION
Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. PROBLEMS AND SOLUTIONS IN QUANTUM COMPUTING AND QUANTUM INFORMATION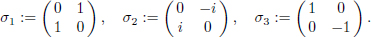 The spin-
The spin- matrix S1, S2, S3 are given by S1 =
matrix S1, S2, S3 are given by S1 = 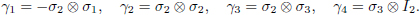 The concept of a Hilbert space will be used throughout the book. A Hilbert space is a set, H of elements, or vectors, (f, g, h,...) which satisfies the following conditions (1) -- (5). (1) If f and g belong to H , then there is a unique element of H , denoted by f + g, the operation of addition (+) being invertible, commutative and associative. (2) If c is a complex number, then for any f in H , there is an element cf of H ; and the multiplication of vectors by complex numbers thereby defined satisfies the distributive conditions
The concept of a Hilbert space will be used throughout the book. A Hilbert space is a set, H of elements, or vectors, (f, g, h,...) which satisfies the following conditions (1) -- (5). (1) If f and g belong to H , then there is a unique element of H , denoted by f + g, the operation of addition (+) being invertible, commutative and associative. (2) If c is a complex number, then for any f in H , there is an element cf of H ; and the multiplication of vectors by complex numbers thereby defined satisfies the distributive conditions  (3) Hilbert spaces H possess a zero element, 0, characterized by the property that 0 + f = f for all vectors f in H . (4) For each pair of vectors f, g in H , there is a complex number f|g, termed the inner product or scalar product, of f with g, such that
(3) Hilbert spaces H possess a zero element, 0, characterized by the property that 0 + f = f for all vectors f in H . (4) For each pair of vectors f, g in H , there is a complex number f|g, termed the inner product or scalar product, of f with g, such that 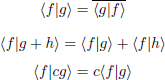 and
and