Martin Gardner - Entertaining Science Experiments with Everyday Objects

Entertaining
Science Experiments

with Everyday Objects

Martin Gardner

Illustrated by
Anthony Ravielli

Dover Publications, Inc.
New York

Copyright 1960, 1981 by Martin Gardner and Anthony Ravielli.

Copyright 1957, 1958, 1959 by Martin Gardner.

All rights reserved.

This Dover edition, first published in 1981, is a slightly corrected republication of the work first published by The Viking Press, N.Y., in 1960, under the title Science Puzzlers. The page of Selected References has been omitted in the present edition.

Library of Congress Catalog Card Number: 81-67088
International Standard Book Number
ISBN-13: 978-0-486-24201-9
ISBN-10: 0-486-24201-3

Manufactured in the United States by Courier Corporation
24201319
www.doverpublications.com

To

M. E. Hurst

a physics teacher

who taught

much more than physics

CONTENTS

In selecting experiments for this volume, I have tried to keep in mind two guiding principles. First, avoid experiments requiring special equipment that cannot be found in an average home. Second, concentrate on experiments that, in addition to being amusing, astonishing, or entertaining, also teach something of importance about science.

Some of the stunts in this book, I must confess, were known to the ancient Greeks, but many are quite new and appear here for the first time inside a book. Who invents these clever diversions? I sometimes suspect that many of them are the brain-children of distinguished scientists who have not lost their boyhood spirit of play. Such a man was Robert W. Wood, a professor of physics at Johns Hopkins University. When he was not working on important projects or writing technical papers, Doctor Wood amused himself by playing practical jokes on his colleagues, exposing pseudo-scientists and spirit mediums, writing science fiction, and helping the police solve bombing mysteries. His quaint little book of drawings and verse, How to Tell the Birds from the Flowers, has been reprinted in paperback (New York: Dover Publications). Perhaps you have seen Paul Winchell, the television ventriloquist, ink a pair of eyes and a nose on his chin. The image of his face is inverted on the screen and Winchell wears on his head a dummys costume that covers all of his face except the mouth and chin. The result is a weird, pinheaded creature with a flexible, gigantic mouth that grins when Winchell frowns and frowns when Winchell grins. This stunt was invented by none other than the fabulous Professor Wood.

Several decades ago, when there was a spirited public debate over whether pitched baseballs could really be made to curve, Wood devised a simple demonstration. He took a large, flat rubber band, cut it to make one long strip, then wound it tightly around a Ping-pong ball. By holding the free end of the band he was able to snap the ball forward, at the same time imparting to it a strong spin. The curving of the balls path was clearly visible. (This stunt was not included in this collection because huge flat rubber bands are hard to come by, but Bernoullis principle, which explains why baseballs curve, is easily demonstrated with a spool and card as explained on page 109).

To get the greatest value from this collection, try to follow up the experiments with exploratory reading. For example, after you have learned how to release a tangled couple (page 49), look up topology in a modem encyclopedia. Better still, read the chapter on it in the fascinating book, Mathematics and the Imagination, by James Newman and Edward Kasner (New York: Simon and Schuster, 1940). Dont just set fire to a lump of sugar (page 19) and then forget about it. See what you can learn about catalysts and the role they play in important chemical changes.

One other suggestion. If you want to entertain your friendsand some of the experiments in this book are superb party stuntspractice them a few times before you demonstrate. Harpooning a raw potato with a soda straw, for instance, is an amazing parlor trick, but you may have to damage many straws before you get the knack. Sherwood Anderson wrote a famous short story, The Triumph of the Egg, about a restaurant owner who failed miserably in trying to show a customer how to put an egg into a bottle (see page 101). If the poor fellow had only practiced his trick a few times, he might not have forgotten what to do to make it work.

If you know, or should you invent, an unusual science experiment that is not in this collection, drop me a note about it in care of the publisher. I cant promise that I will find time to answer your letter, but I shall be most grateful, and perhaps I will be able to use your stunt in a second collection.

M ARTIN G ARDNER

Entertaining
Science Experiments

with Everyday Objects

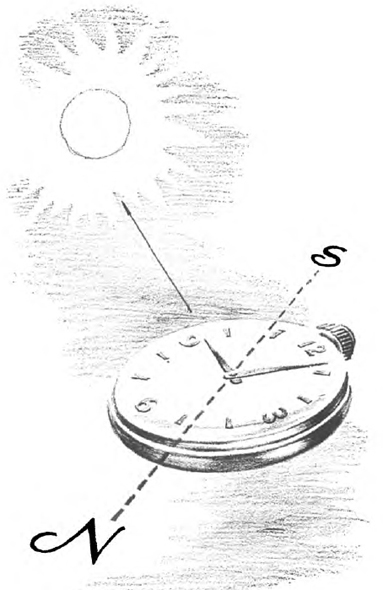
Did you know that a watch can be used as a reliable compass on any day the sun is visible? Simply hold the watch flat and point the hour hand in the direction of the sun as shown. Imagine a line running from the center of the watch through a point midway between the hour hand and the number twelve. This line will point south.

The rule to remember is this: Before twelve noon, you bisect the angle formed by going counterclockwise from the number twelve to the hour hand. After twelve noon, you bisect the angle formed by going clockwise from the number twelve to the hour hand.

A little astronomical reflection should make clear why this works. In our hemisphere, the sun is due south at noon. If at that time we point the hour hand at the sun, both the hand and the number twelve will point south. Before that time, the sun will lie counterclockwise from the number twelve, and after that time, clockwise. During the twenty-four hours from twelve noon to twelve noon, the sun will make a complete circle back to its starting point, but the hour hand will make two circles in the same direction around the dial. Thus, the distance the hour hand travels, and the angle determined by its travel, must be halved.

On the other side of the equator the number twelve must be pointed at the sun. The angle between this number and the hour hand will then indicate north.

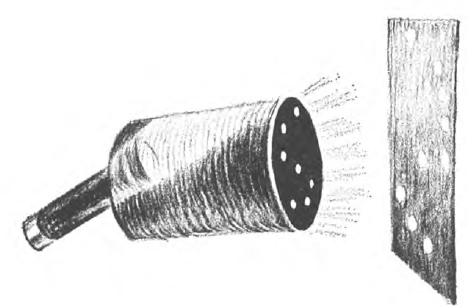
Cylindrical cardboard boxes, of the type at least one brand of oatmeal comes in, can be used for projecting beautiful images of star constellations on the wall or ceiling. Copy the constellation you wish to study on a sheet of thin paper. (You can find star charts in books on astronomy or accompanying an article on constellations in an encyclopedia.) Place the drawing face down on the outside of the bottom of the box. You should be able to see the star dots through the paper. With a nail, punch holes through the box at each dot. These holes form a mirror-image pattern of the constellation, but it will appear normal when projected.

To operate your planetarium, take it into a dark room and insert a flashlight into the open end. Tilt the flashlight so it shines against the side of the box rather than directly toward the holes. This will throw an enlarged image of the constellation on the wall. By turning the box you can study all positions of the configuration.

How many times does the earth rotate during one complete journey around the sun? The answer depends on your point of view. As seen from the sun, the earth makes 365 turns. But as seen from a fixed star, it rotates 366 times. So the sidereal day (a rotation relative to a star) is a bit shorter than a solar day.