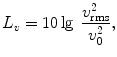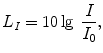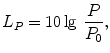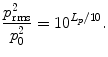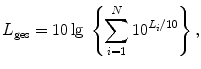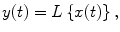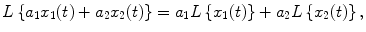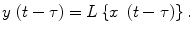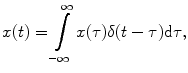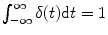1.1 Introduction
Sound consists in mechanical vibrations within the frequency band of human hearing from approximately 16 Hz16 kHz. Vibrations in air and in liquids are called airborne and liquid-borne sound respectively, vibrations in solids are called structure-borne sound.
For further fundamentals on Technical Acoustics, see, for example, [].
1.2 Level and Measurement Quantities
For airborne sound, the primary quantity is the sound pressure, which is determined using microphones () are based on several microphones. For structure-borne sound, the surface displacements , their velocity v =/ t or their acceleration a = v / t are determined.
In view of Webers and Fechners law, stating that the human perception is proportional to the logarithm of the stimulus, the physical quantities are usually expressed in terms of their levels. The sound pressure level L p is defined to be
where p eff denotes the root mean square value of the signal
and the standardized reference is p 0=2105 N/m2. Human beings perceive sound pressures approximately between p rms= p 0 (threshold of audibility) and p rms= 200 N/m2 (threshold of pain). The atmospheric pressure amounts to about 105 N/m2; the sound pressures therefore are comparatively very small. The human perception comprehends approximately 0< L <140 dB. The pseudo unit decibel is used for the outcome of Eq. (). 1 dB corresponds to the threshold of audible difference between two pressures. 10 dB correspond approximately to the doubling of stimulus.
The quantities local velocity v , temporally averaged intensity I and power P (see Sects. ) also are described by their levels. They are defined in such a way, that equal level values result for the case of plane propagating waves with v = p / p 0 c and
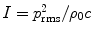
( 0c=characteristic impedance of air = 400 kg/s/m2)
and
with v 0= p 0/ 0 c =5108 m/s, I 0= p 02/ 0 c = 1012 W/m2 and P 0= I 0 1 m2=1012 W. As mentioned, L p = L v = L I = L P holds for plane propagating waves ( L P denotes the level of the power through an area of 1 m2).
Often several incoherent signals (incoherent means signals with different frequency components, for example, two cars or two noise sources, etc.) with known partial levels have to be combined to a total level. In such cases, the single mean square values have to be calculated from the inverse of Eq. ()
The total mean square value equals the sum of partial ones; therefore, the total level equals
( L i : partial levels, N : their number). Equation () says, for example, that a second source with the same level yields a 3 dB increase, that three equal one third octave band levels are 4.8 dB lower than the corresponding octave band level and that a 6 dB signal to noise ratio results in an error of 1 dB.
1.3 Fundamentals of System Theory
Acoustical transducers and vibrating structures may be described by a cause-effect-chain, which often is called the system. An excitation x ( t ) (also named the system input) causes vibrations of a dynamical structure, which can be observed at a certain point using some appropriate quantity y ( t ) (being the system output). Examples are the input voltage x ( t ) for a loudspeaker in an arbitrary acoustical environment and the output voltage y ( t ) of a microphone observing the sound field; or force signals x ( t ) exciting structures like beams and plates somewhere to result in some response y ( t ). Literature on system theory can be found for example in [].
For sufficiently small amplitudes, acoustical transducers behave LINEARLY; this is, for example, true for airborne sound below 130 dB. Linear simply means that the principle of superposition is valid. If the operator L denotes the transformation of the input signal accomplished by the system in question to give the output signal
then LINEAR transduction is described by the fact
( a 1, a 2: constants, x 1, x 2: arbitrary signals).
In addition, systems are called time invariant, if their reaction after a time shift of the input also only results in the same time shift of the output:
Linear and time-invariant transducers are easily described using their impulse responses h ( t ) or their transfer functions H (); dropping one of these assumptions causes often a difficult and complex description of the system. The assumptions of linearity and time invariance are of course not self-evident in general, but may be assumed in many cases; appropriate experiments have to be carried out, if needed.
1.3.1 Description with Impulse Response Function
The simple mathematical fact that all signals may be represented by a comb of delta functions (Diracs comb)
(( t )=Diracs delta function with ( t 0)=0 and
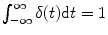











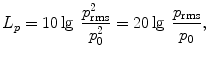
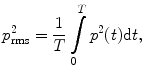
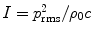 ( 0c=characteristic impedance of air = 400 kg/s/m2)
( 0c=characteristic impedance of air = 400 kg/s/m2)