Inga Johnson - An Interactive Introduction to Knot Theory

An Interactive Introduction to

Inga Johnson

Willamette University

Allison Henrich

Seattle University

DOVER PUBLICATIONS, INC.
Mineola, New York

Copyright

Copyright 2017 by Inga Johnson and Allison Henrich

All rights reserved.

Bibliographical Note

An Interactive Introduction to Knot Theory is a new work, first published by Dover Publications, Inc., in 2017.

International Standard Book Number

ISBN-13: 978-0-486-80463-7

ISBN-10: 0-486-80463-1

Manufactured in the United States by LSC Communications

80463101 2017

www.doverpublications.com

This book does not follow the design of a traditional math textbook. There are very few complete proofs included, and the exercises are not listed at the end of each section. Instead, this text is an invitation to ponder, question, create, and figure out on your own some beautiful mathematical results in the field of knot theory. Exercises are sprinkled in between statements of definitions, descriptions, and propositions. Some exercises are designed to introduce you to new ideas and to point you in the direction of why or how an idea is important. Other exercises guide you through the technical and subtle arguments that provide the foundation for our understanding of knots and links. Answers are rarely provided in full, but the path toward a solution or proof is illuminated.

As indicated by the word interactive in the title, this book is meant to be read with paper and pencil (colored pencils, string, and pipe cleaners, too!) in hand so that you can jot down your ideas, explore how a new definition applies to your favorite examples, find the answer to a question, or prove a theorem. As you are reading the text, we hope you will be in a space where conversations and collaborations with others are readily available.

We designed this book for a student-centered classroom where students regularly spend class time working collaboratively on problems, presenting solutions, and vetting arguments made by their peers. We have used the textbook both in a 10-week quarter and in a 15-week semester. Our classes typically have 10-20 undergraduate students, though this book could be used by a larger class of up to 30 students or even by a single group of 2-3 undergraduate research students. Indeed, we have successfully used parts of the book to introduce summer research students to the fundamental ideas in knot theory. Prerequisites for this book include a course on proof writing (which includes exposure to ideas like sets and modular arithmetic) and proof techniques (e.g., proof by induction) as well as a course on linear or matrix algebra.

to allow time to first play and build intuition within the mathematically rich and beautiful field of knot theory.

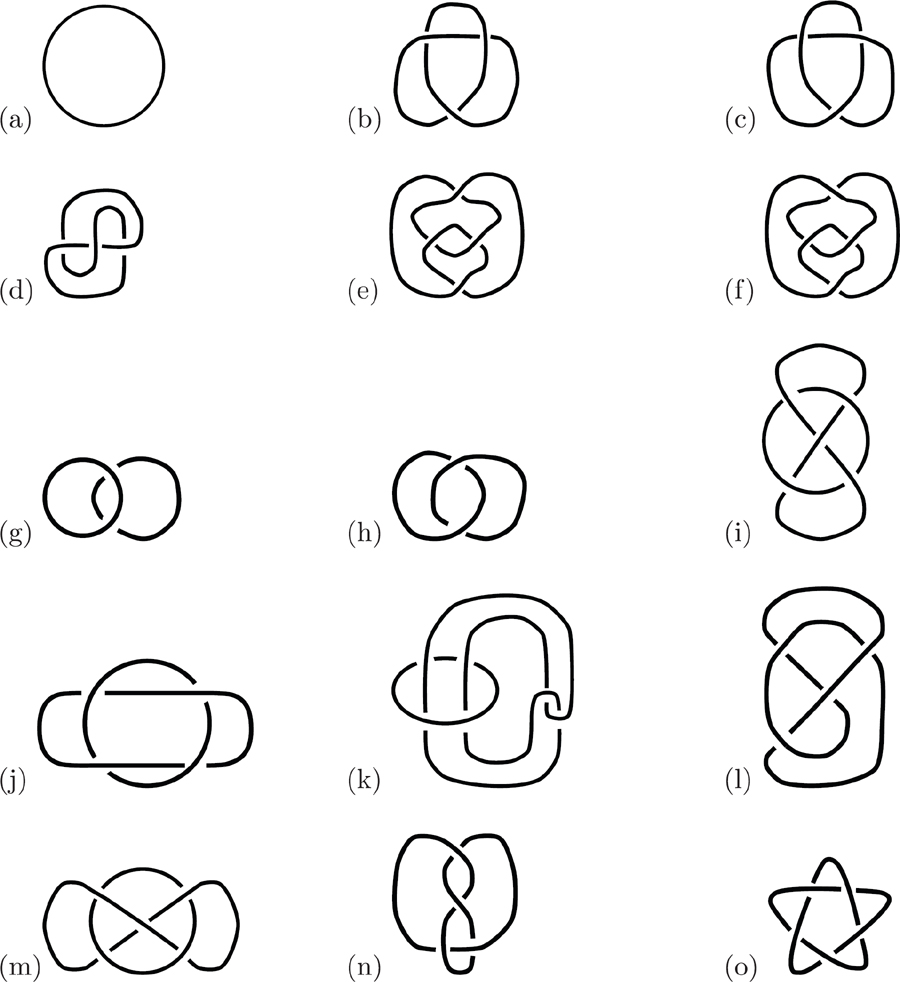
Informally, a knot is a closed loop in space. The term closed loop means that the loop has no loose ends, and no beginning or ending points. You can think of a knot as a knotted-up circle made of string or wire. A link is a collection of closed loops in space and the number of loops is called the number of components of the link. A link can have one component. Thus, knots are just special types of links having only one component. Note that, when we use the term link in this book, we are generally referring to both knots and links with more than one component.

The examples of knots and links seen in are flat drawings of 3-dimensional loops in space. A 2-dimensional drawing of a link is called a diagram of the link. In a diagram, the term crossing is used to describe a location where one portion of the link passes over another portion of the link. Crossings are identified by a short break in the drawing of the curve, which indicates that this portion of the curve is passing under the unbroken portion of curve.

Two links are called equivalent if they have the same number of components and they can be physically manipulated in space (rotated, bent, twisted, stretched, etc.), without cutting, so that the first link is transformed identically into the second. We imagine that our strings are highly elastic so they can be scaled up or down in size, stretched and contracted.

While playing and building your intuition with the activities in this chapter, you may come up with your own questions or conjectures. We encourage you to collect and write down your ideas and add them to the list of questions in . Perhaps you will create your own new open research question about knots or perhaps you will stumble upon the same questions that the founders of the field of knot theory have puzzled over for years.

One last note before you begin. In mathematics, formal proofs of theorems rely on concepts and constructions being formally defined. Since the formal definition of a knot is not given in , you will notice a shift from play to formalism. Formal proofs related to the definition of a knot or link will serve as the foundation both for our play and for our proofs in the remainder of the book.

Table 1.1: Examples of Link Diagrams.

. Build them with pipe cleaners, and determine any equivalences between different pictures. Record your findings and conjectures.

Given a link L in space and a light source some distance away, the shadow of the link made on a plane across from the light source is called a projection or shadow of the link. Projections can look similar to the pictures in , but they are missing information about which is the under-strand and which is the over-strand. The curve intersections in a projection are called precrossings. A precrossing is said to have been resolved once we have selected the crossing information (that is, we have specified which strand passes over and which passes under at the crossing). Once all crossing information is determined in a link projection, the image is then a link diagram.

Figure 1.1.1: A knot projection in a plane, the knot in space, and a light source.

The projection of a link L onto two distinct planes in can result in strikingly different images. Some projections are nonstandard and cannot .) Two different projections of a link, L, can also have vastly different numbers of crossings. The following two exercises investigate the relationship between a link, its numerous projections, and the diagrams stemming from those projections.

Exercise 1.1.2. (a) Make a knot out of rigid material such as wire. Draw a projection of that knot from two perspectives that result in significantly different projections. (b) For that same knot, draw a nonstandard diagram of your knot from which the knot cannot be reconstructed. (For instance, maybe there are places in your diagram where several strands are tangent to each other or where three or more strands of the knot intersect at a single point.)