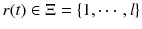1.1 Research and Development Status of Generalized Markov Jump Linear System Theory
1.1.1 Basic Model of Generalized Markov Jump Linear Systems
The research of switched systems is mainly carried out with the research of hybrid systems []. A hybrid system is a dynamic system that exhibits both continuous and discrete dynamic behaviora system, such as manufacturing systems, weather forecast systems, power systems, biological systems, as well as option pricing models in financial engineering, insurance surplus distribution models, multi-sector fixed asset dynamic input-output models, etc., that can both flow (described by a differential equation) and jump (described by a state machine or automaton). In the process of its operation, a hybrid system often suffers from a sudden change in the environment, internal connection changes between each subsystem in a large system, changes of nonlinear objects, damages of the system components and random mutations, such as human intervention. These phenomena can be seen as a response of the system driven by a class of random events. In general, the state of such a system is defined by the values of the continuous variables and a discrete mode. The state changes either continuously, according to a flow condition, or discretely according to a control graph. Continuous flow is permitted as long as so-called invariants hold, while discrete transitions can occur as soon as given jump conditions are satisfied. Discrete transitions may be associated with events. Such systems are often called hybrid systems in control theory.
When the discrete event of hybrid systems is characterized by discrete switching signals, such important systems are called jump systems. This kind of systems can be described by finite subsystems or dynamic models, and at the same time there is a switch law, which makes the switching between various subsystems.
A stochastic jump system can usually be described by the following state equations:
where
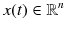
is a continuous variable,
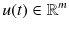
is an external signal of continuous control input or continuous dynamic systems,
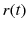
is a piece-wise constant function valued in a finite set
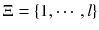
, usually referred as switch signals, or switching strategy of the system.
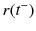
indicates that
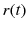
is a piece-wise constant right hand continuous function. When
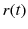
takes different values, the system ().
A generalized stochastic jump system is usually described by the following state equations:
where
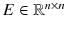
is a known singular matrix with 0 < rank( E ) = k n ,
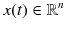
,
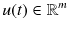
,
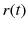
,
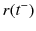
,
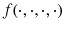
,
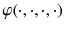
are the same as system ().
This book is focused on a kind of special jump systems with Markov switching parameters, which is known as Markov jump systems. In such systems, the switching rules determine which corresponding subsystem the system would be switched to at each moment, and the state of the system would be switched to the corresponding state at the corresponding moment. But during the process of the system switching from one mode to another mode, there is no switching rule to obeying, and the switching process between different modes is random. This kind of random switching accords with some certain statistical propertiesthe transformation among various regime of the discrete event finite set of the system is a Markov jump process, therefore, it can be also regarded as a special case of stochastic systems, called stochastic Markov switching systems (also known as stochastic Markov jump systems, or stochastic Markov modulation systems).
A Markov jump system is constructed by two parts. One part of the system is the state of the system, and the other part is the system mode, which depends on the Markov process, deciding the execution of the subsystem at a certain moment, in order to control and coordinate the normal operation of the whole system.
- (1)
Mathematical Model of Continuous Generalized Markov Jump Systems
The continuous generalized stochastic Markov jump linear system is described as:
where
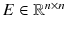
,
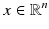
,
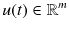
are the same as system (), and the switch signals or switching strategy of the system
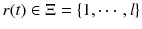












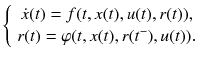
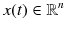 is a continuous variable,
is a continuous variable, 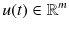 is an external signal of continuous control input or continuous dynamic systems,
is an external signal of continuous control input or continuous dynamic systems, 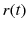 is a piece-wise constant function valued in a finite set
is a piece-wise constant function valued in a finite set 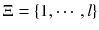 , usually referred as switch signals, or switching strategy of the system.
, usually referred as switch signals, or switching strategy of the system. 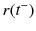 indicates that
indicates that 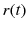 is a piece-wise constant right hand continuous function. When
is a piece-wise constant right hand continuous function. When 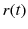 takes different values, the system ().
takes different values, the system ().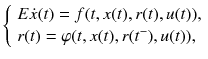
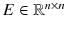 is a known singular matrix with 0 < rank( E ) = k n ,
is a known singular matrix with 0 < rank( E ) = k n ,  ,
,  ,
, 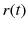 ,
, 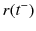 ,
, 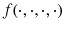 ,
, 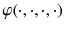 are the same as system ().
are the same as system ().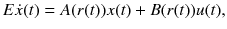
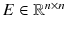 ,
, 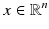 ,
, 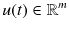 are the same as system (), and the switch signals or switching strategy of the system
are the same as system (), and the switch signals or switching strategy of the system