Howard - Problem-Solving: the Owners Manual

D ecision making is goal oriented. That is, we make decisions in order to achieve objectives or solve problemsmaking a decision is a means to an end. This chapter explores techniques, tools, and approaches that take into account the ways our brains work and how we really think. The word problem comes from the Greek pro- , forward, and ballein , to throw or drive; it means something made to go forward, as when something is stuck and incapable of movement and is in need of returning to forward movement. Problems include disease, malfunction, disagreement, and mysteryall conditions in which movement is denied, in which the parties are stuck and in need of some solution that enables a return to forward movement. When you have a problem, you cant just keep doing business as usual. You must do something that is not normally a part of your routine; special attention is required to get things unstuck.

Before plunging into the details of problem-solving styles, definitions, and techniques, I want to make one point perfectly clear: the best problem solver is an expert in the subject involved. An expert might be an engineer, a consultant, a professor, a competitor, or even someone who knows the task intimatelythe worker. No technique is as good as an expert. So, depending upon the seriousness of the problem, consult an expert before trying one of these techniques. For example, if youve got a cold, treat yourself, but if the symptoms are more complex, consult an expertyour doctor. The techniques mentioned in this chapter are intended to serve either (1) when relevant expertise is unavailable or (2) when the experts have been stumped. I was once called in to help solve a problem that had stumped the experts for about nine months. A $500,000 machine had been failing in the field 50 percent of the time. By applying the right technique (root-cause analysis, described by Plunkett and Hale, 1982), I led a group of 10 experts, and we found the cause of the problem in six hours.

Over the last 20 years or so, attempts to define problem-solving styles have flourished. These styles are all based on various combinations of personality traits (see the Big Five traits discussed in chapter 30). The literature on problem-solving styles is extensive, and I will not treat it here. Suffice it to say that all the attempts at defining styles are based on extreme scores on the Big Five. Four of the ten possible Big Five extreme scores appear to be most commonly associated with problem-solving style:

1. The preserver (low Originality) looks for a quick solution based on tried-and-true principles.

2. The explorer (high Originality) aims at an innovative solution based on a new insight.

3. The challenger (low Accommodation) goes after the truth by using unrelenting logic, letting the chips fall where they may.

4. The adapter (high Accommodation) seeks harmony and buy-in by building consensus.

Basadur, Graen, and Wakabayashi (1990) offer an alternative based on one of the above Big Five dimensions (Originality) and one different one (Consolidation). According to their model, four problem-solving styles emerge based on these combinations of extreme scores:

1. Implementer: low Originality + high Consolidation

2. Generator: low Originality + low Consolidation

3. Optimizer: high Originality + high Consolidation

4. Conceptualizer: high Originality + low Consolidation

Applications

When you are faced with a problem of some magnitude, consider which style is most relevant to understanding and solving it. For many complex problems, a combination of all the styles is particularly powerful.

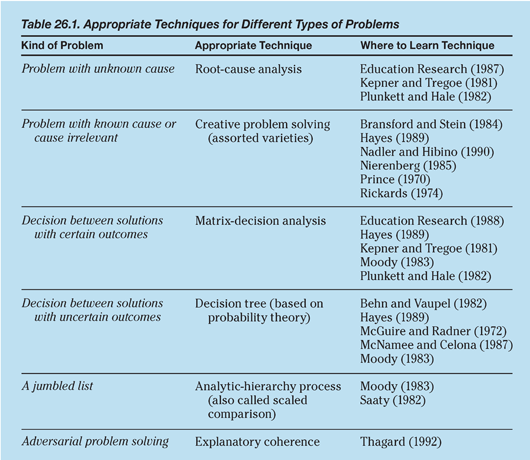
To assess your own style and the styles of those around you, use the worksheet in appendix F to find the Big Five trait descriptors most typical of you and yours, or you might contact the publishers of the tests and models identified in table 26.1.

When you are assembling teams to solve problems, encourage diversityin personality, styles, expertise, departmental experience, and so on. (Contributed by Rick Bradley)

The diversity recommended in application 3 may also help with general acceptance of the teams solution to the problem afterward. (Contributed by Jane Howard)

At the highest level of thinking about problems, two kinds of problems appear:

1. Problems for which the possible solutions are unknown (as in Why is my car not starting?)

2. Problems for which the solutions are known, but the best solution is not obvious (as in Which employee should I assign to this project?)

The goal in solving the first type of problem is to generate ideas, whereas the goal in solving the second type is to make a decision, or to select from among available ideas.

Problems for which the solution is unknown can be further subdivided into two categories:

1. Problems where the cause is unknown and must be discovered

2. Problems where the cause is known, or is unknown and irrelevant

An example of the first category would be a blown fuse or a tripped circuit breaker. If you do not discover the cause of the electrical overload, you risk fire (at most) or the unavailability of that electrical circuit (at least). An example of the second category would be having a flat tire in the desert with no jack available. The cause of the flat is most likely irrelevant; you just need some good ideas.

Problems for which the best solution is not obvious can be subdivided into three categories. Although these situations are frequently referred to (erroneously, I think) as problems, they are more aptly called decisions. The verb decide comes from the Latin de- (off) and caedere (to cut), or to cut off. In other words, decision time is the time to cut off debate and affirm the solution to the problem at hand. In its purest form, then, a problem is a mess without a solution, and a decision situation is a mess with two or more possible solutions. The three classes of solution are

1. Solutions with certain outcomes

2. Solutions with uncertain outcomes

3. Solutions in need of being prioritized

An example of the first type is deciding which home to buy; the outcome is certain, in the sense that its features are plain to the eye. An example of the second type is deciding whether or not to risk major surgery; the outcome is unknown, although to some degree it is predictable. The third type could be having a list of 20 projects that need to be undertaken, yet having a budget for only a few of them.

Applications

When you commit to trying to solve a problem, first determine what kind of problem it is. Once you know that, you will know your objective. This information is summarized in table 26.2.