Dennis Sentilles - A Bridge to Advanced Mathematics

Copyright
Copyright 1975, 2011 by Dennis Sentilles
All rights reserved.

Bibliographical Note

This Dover edition, first published in 2011, is an unabridged republication of the work originally published by The Williams & Wilkins Company, Baltimore, in 1975. A new preface by the author has been specially prepared for this edition.

Library of Congress Cataloging-in-Publication Data

Sentilles, Dennis.

A bridge to advanced mathematics / Dennis Sentilles.

p. cm.

Originally published: Baltimore : Wilkins, 1975.

Summary: This helpful bridge book offers students the foundations they need to understand advanced mathematics, spanning the gap between practically oriented and theoretically oriented courses. Part 1 provides the most basic tools, examples, and motivation for the manner, method, and material of higher mathematics. Part 2 covers sets, relations, functions, infinite sets, and mathematical proofs and reasoning. 1975 editionProvided by publisher.

Includes bibliographical references and index.

ISBN-13: 978-0-486-48219-4 (pbk.)

ISBN-10: 0-486-48219-7 (pbk.)

1. Proof theory. 2. ArithmeticFoundations. I. Title.

QA9.S44 2011

511.36dc22

2011002266

Manufactured in the United States by Courier Corporation
48219701
www.doverpublications.com

It is surprising that this little book has survived all these years to reappear now thanks to the interest of Dover Publications. It was first written at almost the very moment when the next generation of prospective mathematics students became the first generation to turn instead toward computer science, a fate that might well have appealed to its author, had he been born but a very few years later. There seems not that much difference in satisfaction to be found between devising a beautiful proof or devising a beautiful program, except for greater immediacy of reward in the latter. These endeavors both demand rigor of mind applied to abstract conception that is largely existent at first only in the imagination. Experience in one is surely valuable to the other. But that seems the extent of it.

A fundamental mathematical result endures forever, the Pythagorean Theorem being perhaps the oldest example. A good mathematical result is a hard, solid thing, established via a demanding methodology, even as it exists only in the mind, valid wherever and whenever its underlying assumptions occur. That is what this book is about and I hope still serves: basic foundations and an introduction to the rigor of the fundamental methodology. Such a study was the great pleasure of my undergraduate studies.

Paul Cohens work on the Continuum Hypothesis made it just barely into the original pages of this book. Since their writing, the 4-Color Problem, Fermats Last Theorem, and the Poincar Conjecture have all fallen to the mathematicians mind. Other than these advances, almost all of its contents serve as currently now as it did then.

To pull together what so many superior minds had done, so that another mind might immerse in it tooit was a labor of love, a happy moment that I was privileged to have had all those years ago.

D ENNIS S ENTILLES
Professor Emeritus of Mathematics
The University of Missouri

This text is what its title claims. A bridge to be crossed by the student of mathematics in his (usually) third semester of the university curriculum. Its intent is to span the gap that exists between a practically oriented calculus sequence and the theoretically oriented courses in algebra, analysis and other areas which typically follow in his third and fourth years.

I came to this course and the writing of this text by way of two experiences. The first was that I had taken such a course in the foundations of mathematics as an undergraduate and found it to be the most interesting and one of the most valuable of my studies. The second was my experience in attempting to teach advanced calculus to mathematics students who had no real idea of what post-18th century mathematics was like, in neither its techniques nor interests. I thought this was a disservice to students who were about to commit their third or even fourth year to the subject, including both those who would go on and those who needed to realize that core mathematics was not really what interested them. Hence I began teaching a course intended to bridge the gap between the procedural courses of the first year and conceptual courses of the later years, to be taken immediately following or concurrently with the last semester of basic calculus.

My colleagues and I both felt that the students leaving such a course should have a basic acquaintance with proof in mathematics, an awareness of what modern mathematics was like, and a sure knowledge of basic logic, set theory, relations, functions, and the real and natural number systems. I also thought that the students might profit from and enjoy some discussion and study of how mathematics got to be the way it is, an appearance quite different from what they imagined. Hence one finds in this text a few sections on the history and development of mathematics and the reasons for and uses of axiom systems. These ideas framed the basic course; it has considerably evolved from this earliest conception.

I found it necessary to devote more time to logic than I wished, one week to basic symbolic logic and one week to the uses of quantifiers and the actual meaning of mathematical statements. In response to the suggestions of several anonymous and very helpful reviewers, can be referred to for further explanation of details of logic encountered in use in later chapters.

and are likely to be more meaningful to the student.

around Question I or II, or both, will, I believe, not be felt strongly enough to be effective toward any significant realization on the students part unless the instructor constantly keeps the Question before the student and shows how each new topic relates in some close way to some detail of the Question or Questions posed and shows how in the end these topics all come together to provide a definitive answer.

This brings up a final key decision about the content of this text. I wished to teach the art of mathematical proof. I needed a subject which was clear enough to allow easy concentration on the details and techniques of proof itself, while at the same time was abstract enough to allow a valid introduction to modern mathematics. I also wished to be able to say to these sophomores that this mathematics was at least of their own century, albeit before their time. But I also needed a subject that could be well founded intuitively so that I could easily motivate concepts and definitions and could easily manifest in a clear manner the meaning of results that were stated and proven most abstractly. Many texts meet this goal by choosing some subject from modern algebra or linear algebra or choose to develop the real number system. I felt that these approaches have two faults. One is that the student already knows a little about the subject and persists in cluttering up the development with half-forgotten memories of high school or college algebra. 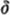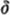Another is that these subjects provide minimal aid in the upcoming confrontation with modern analysis, differential equations, advanced applied mathematics and probability, with their bewildering requirements of for every e there is a and their necessity to operate constantly with inequality, approximation, and the technique of making uncertainty certain. One subject that I felt would meet all these problems was basic point set topology. Topology is not the subject of . Topology is the glue that holds together the mix of all those topics and techniques and ways of mathematical thought that I wished to introduce. (My own experience with point set topology is that it is a good place to learn to think, write and speak in mathematics.) The students have found topology interesting, have been able to prove theorems in it and, as one student remarked, come to see that mathematics exists and can be done without number, direction or measurement. Pedagogically, topology has the strong point of enabling the student to actually see the need for, and the use of, the for every and there exist quantifiers, a point that, from my experience, presents considerable difficulty.