Blaise Pascal - Collected Works of Blaise Pascal

The Collected Works of

BLAISE PASCAL

(1623-1662)

Contents

Delphi Classics 2020

Version 1

Browse our Main Series

Browse our Ancient Classics

Browse our Poets

Browse our Art eBooks

Browse our Classical Music series

The Collected Works of

BLAISE PASCAL

By Delphi Classics, 2020

Collected Works of Blaise Pascal

First published in the United Kingdom in 2020 by Delphi Classics.

Delphi Classics, 2020.

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission in writing of the publisher, nor be otherwise circulated in any form other than that in which it is published.

ISBN: 978 1 91348 725 6

Delphi Classics

is an imprint of

Delphi Publishing Ltd

Hastings, East Sussex

United Kingdom

Contact: sales@delphiclassics.com

www.delphiclassics.com

Explore Philosophy at Delphi Classics

Clermont-Ferrand, a city in the Auvergne-Rhne-Alpes region of central France Pascals birthplace

Cathedral Notre-Dame de lAssumption, Clermont-Ferrand

Pascal was born in the crowded medieval centre of Clermont-Ferrand

A nineteenth century depiction of Pascals birthplace, which no longer stands

Translated by Frances Marguerite Clarke

(Translated from the French by Dr. Frances Marguerite Clarke, Bryn Mawr College, Bryn Mawr, Penna.)

W HEN PASCAL WAS only sixteen years old, he wrote a brief statement which was doubtless intended by him as the first step in an extended study of conics to be undertaken at some future time. In the following year it was printed in the form of a broadside and bore the simple title, Essay pour les coniqves. Par B. P. Of this single page only two copies are known, one at Hannover among the papers of LEIBNIZ, and the other in the Bibliothque nationale at Paris. The illustrations here given appeared at the top of the original broadside. The third lemma involves essentially the Mystic Hexagram of Pascal. This translation first appeared in Isis, X, 33, with a facsimile of the entire essay, and is reproduced in revised form with the consent of the editors.

First Definition

When several straight lines meet at the same point, or are parallel to each other, all these lines are said to be of the same order or of the same ordonnance , and the totality of these lines is termed an order of lines, or an ordonnance of lines. [This definition is taken almost word for word from DESARGUES. See the notes to the BRUNSCHVICG and BOUTROUX edition, t. I., Paris, 1908. This translation is made from the facsimile of the original as given in this edition, and acknowledgment is hereby made of the assistance rendered by these notes in determining the meaning of several passages. It should also be said that the text of this edition is in marked contrast to the imperfect one given in the Paris edition of 1819.]

Definition II

By the expression conic section, we mean the circle, ellipse, hyperbola, parabola, and an angle; since a cone cut parallel to its base, or through its vertex, or in the three other directions which produce respectively an ellipse, a hyperbola, and a parabola, produces in the conic surface, either the circumference of a circle, or an angle, or an ellipse, a hyperbola, or a parabola.

Definition III

By the word droite (straight) used alone, we mean ligne droite (straight line).

[In this translation, the word line, meaning a straight line-segment, will be used for droite.]

Lemma I

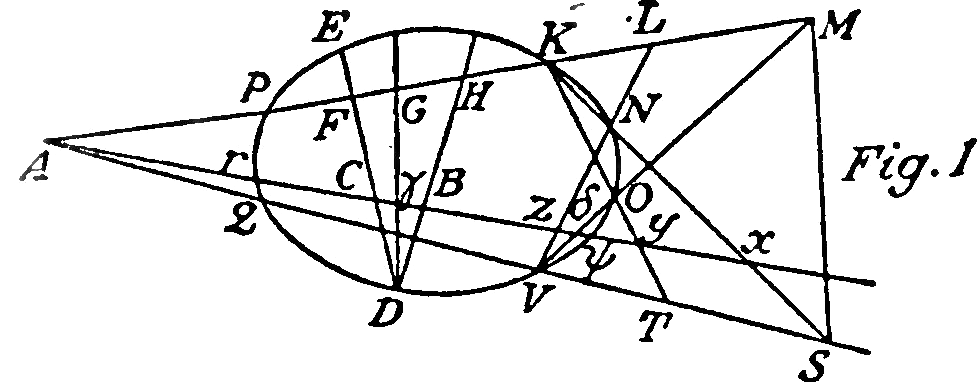
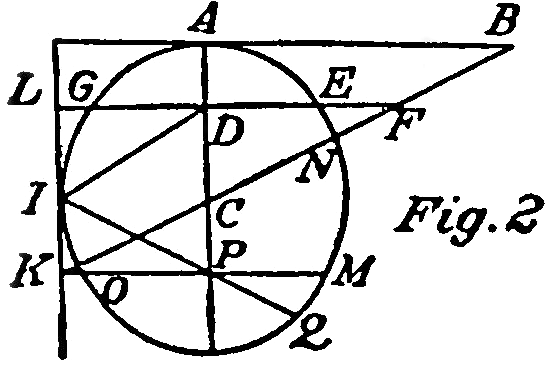
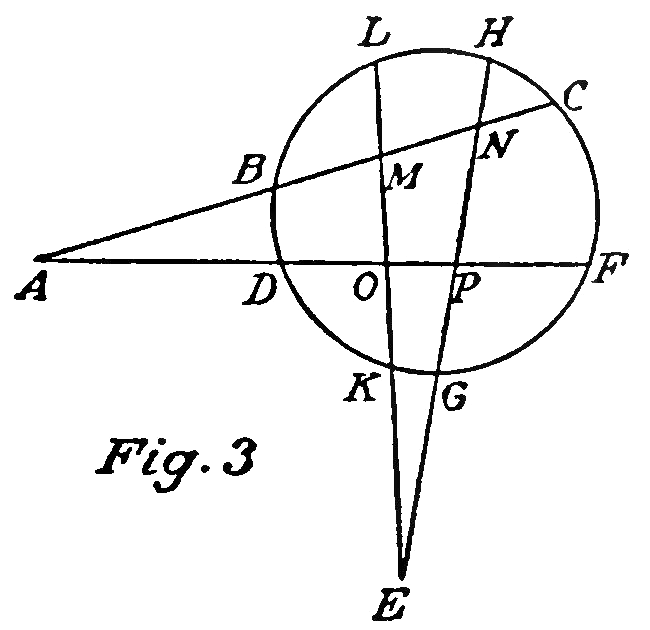
If in the plane M, S, Q, two straight lines MK, MV, are drawn from point M and two lines SK, SV from point S; and if K be the point of intersection of the lines MK, SK; V, the point of intersection of the lines MV, SV; A, the point of intersection of the lines MA, SA; and , the point of intersection of the lines MV, SK; and if through two of the four points A, K, , V, which can not lie in the same line with points M, S, and also through points K, V, a circle passes cutting the lines MV, MP, SV, SK at points O , P, Q, N, then I say that the lines MS, NO, PQ, are of the same order.