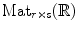Daniel Bump Graduate Texts in Mathematics Lie Groups 2nd ed. 2013 10.1007/978-1-4614-8024-2_1
Springer Science+Business Media New York 2013
1. Haar Measure
Abstract
If G is a locally compact group, there is, up to a constant multiple, a unique regular Borel measure L that is invariant under left translation. Here left translation invariance means that ( X ) = ( gX ) for all measurable sets X .
If G is a locally compact group, there is, up to a constant multiple, a unique regular Borel measure L that is invariant under left translation. Here left translation invariance means that ( X ) = ( gX ) for all measurable sets X . Regularity means that
Such a measure is called a left Haar measure . It has the properties that any compact set has finite measure and any nonempty open set has measure > 0.
We will not prove the existence and uniqueness of the Haar measure. See for example Halmos [] for a proof of this. Left-invariance of the measure amounts to left-invariance of the corresponding integral,
for any Haar integrable function f on G .
There is also a right-invariant measure, R , unique up to constant multiple, called a right Haar measure . Left and right Haar measures may or may not coincide. For example, if
then it is easy to see that the left- and right-invariant measures are, respectively,
They are not the same. However, there are many cases where they do coincide, and if the left Haar measure is also right-invariant, we call G unimodular .
Conjugation is an automorphism of G , and so it takes a left Haar measure to another left Haar measure, which must be a constant multiple of the first. Thus, if g G , there exists a constant ( g ) > 0 such that
If G is a topological group, a quasicharacter is a continuous homomorphism
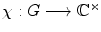
. If |( g )| = 1 for all g G , then is a (linear) character or unitary quasicharacter .
Proposition 1.1.
The function
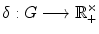
is a quasicharacter. The measure (h) L (h) is right-invariant.
The measure
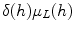
is a right Haar measure, and we may write
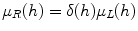
. The quasicharacter is called the modular quasicharacter.
Proof.
Conjugation by first g 1 and then g 2 is the same as conjugation by g 1 g 2 in one step. Thus
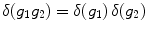
, so is a quasicharacter. Using (),
Replace f by f in this identity and then divide both sides by ( g ) to find that
Thus, the measure
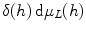
is right-invariant.
Proposition 1.2.
If G is compact, then G is unimodular and
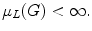
Proof.
Since is a homomorphism, the image of is a subgroup of
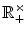
. Since G is compact, ( G ) is also compact, and the only compact subgroup of
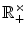
is just
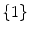
. Thus is trivial, so a left Haar measure is right-invariant. We have mentioned as an assumed fact that the Haar volume of any compact subset of a locally compact group is finite, so if G is finite, its Haar volume is finite.
If G is compact, then it is natural to normalize the Haar measure so that G has volume 1.
To simplify our notation, we will denote
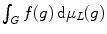
by
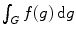
.
Proposition 1.3.
If G is unimodular, then the map
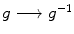
is an isometry.
Proof.
It is easy to see that
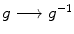
turns a left Haar measure into a right Haar measure. If left and right Haar measures agree, then
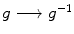
multiplies the left Haar measure by a positive constant, which must be 1 since the map has order 2.
Exercises
Exercise 1.1.
Let
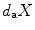
denote the Lebesgue measure on
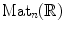
. It is of course a Haar measure for the additive group
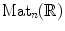
. Show that
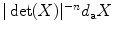
is both a left and a right Haar measure on
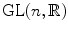
.
Exercise 1.2.
Let P be the subgroup of
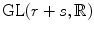
consisting of matrices of the form
Let d g 1 and d g 2 denote Haar measures on
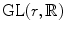
and
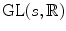
, and let
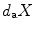
denote an additive Haar measure on
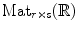











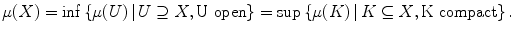
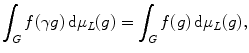
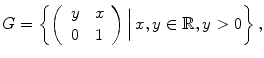

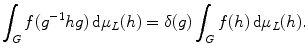
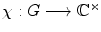 . If |( g )| = 1 for all g G , then is a (linear) character or unitary quasicharacter .
. If |( g )| = 1 for all g G , then is a (linear) character or unitary quasicharacter .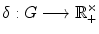 is a quasicharacter. The measure (h) L (h) is right-invariant.
is a quasicharacter. The measure (h) L (h) is right-invariant.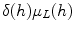 is a right Haar measure, and we may write
is a right Haar measure, and we may write 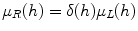 . The quasicharacter is called the modular quasicharacter.
. The quasicharacter is called the modular quasicharacter.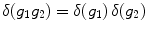 , so is a quasicharacter. Using (),
, so is a quasicharacter. Using (),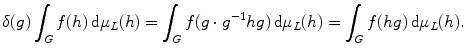
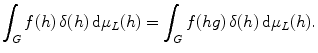
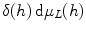 is right-invariant.
is right-invariant.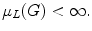
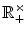 . Since G is compact, ( G ) is also compact, and the only compact subgroup of
. Since G is compact, ( G ) is also compact, and the only compact subgroup of 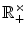 is just
is just 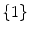 . Thus is trivial, so a left Haar measure is right-invariant. We have mentioned as an assumed fact that the Haar volume of any compact subset of a locally compact group is finite, so if G is finite, its Haar volume is finite.
. Thus is trivial, so a left Haar measure is right-invariant. We have mentioned as an assumed fact that the Haar volume of any compact subset of a locally compact group is finite, so if G is finite, its Haar volume is finite.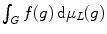 by
by 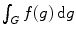 .
.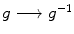 is an isometry.
is an isometry.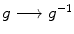 turns a left Haar measure into a right Haar measure. If left and right Haar measures agree, then
turns a left Haar measure into a right Haar measure. If left and right Haar measures agree, then 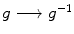 multiplies the left Haar measure by a positive constant, which must be 1 since the map has order 2.
multiplies the left Haar measure by a positive constant, which must be 1 since the map has order 2.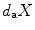 denote the Lebesgue measure on
denote the Lebesgue measure on 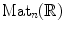 . It is of course a Haar measure for the additive group
. It is of course a Haar measure for the additive group 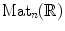 . Show that
. Show that 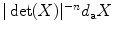 is both a left and a right Haar measure on
is both a left and a right Haar measure on 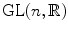 .
.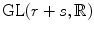 consisting of matrices of the form
consisting of matrices of the form 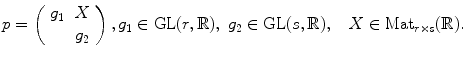
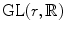 and
and 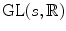 , and let
, and let 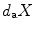 denote an additive Haar measure on
denote an additive Haar measure on