Almossawi - Bad choices: how algorithms can help you think smarter and live happier

D id you know that Richard Feynman started developing the equations that won him the Nobel Prize after seeing someone throw a plate in the air? Or that John von Neumann modeled parts of his electronic computer on a friends idea about how memories are stored in the human brain? Or that the sight of a kicking and screaming orangutan at the zoo led Charles Darwin to his big idea? What Feynman, von Neumann, Darwin, and others have in common is that they see physics and mathematics and science everywhere, way beyond the confines of their laboratories.

Even if youre not gunning for a Nobel Prize, you probably do things in your everyday life that can be modeled as algorithms. In fact, you apply them on a daily basis to solve various problems: finding pairs of socks in a pile of clothes, deciding when to go to the grocery store, determining how to prioritize your tasks for the day, and so on. An algorithm is a series of unambiguous steps that achieves some meaningful objective in finite time. The series might begin with some input and is expected to produce an output. Those are an algorithms characteristics. Whats fascinating is that Babylonian tablets from around 1800 to 1600 BCE reveal that ancient Babylonians wrote down their procedures for determining things like, say, compound interest or the width and length of a cistern given its height and volume using algorithms. That is to say, their procedures were made up of an unambiguous series of steps; they had some input, some output, they eventually terminated and they were useful. Algorithms can thus be found in the works of various contributors to mathematics over the centuries. After the advent of computers, these characteristics have proved crucial because they allow computers to carry out tasks in a way that is predictable.

Despite the importance of algorithms in our lives, texts on the subject tend to focus largely on intricate detailsthe howwhile perhaps ignoring the more practical lessons of those algorithms that make them appealing. The seemingly simple everyday tasks we just mentioned can be undertaken in a number of different ways. The more aware we are of those ways, the better we can hone our ability to achieve a task in the most efficient way. Think of it like enhancing a general-purpose intuition that we all possess. Thats where Bad Choices comes in. This book aims to acquaint you with algorithmic thinking by highlighting different ways of approaching everyday tasks and pointing out how these approaches fare relative to each other. For instance, two methods of looking for a shirt in your size on a rack of shirts might be described like the graph below.

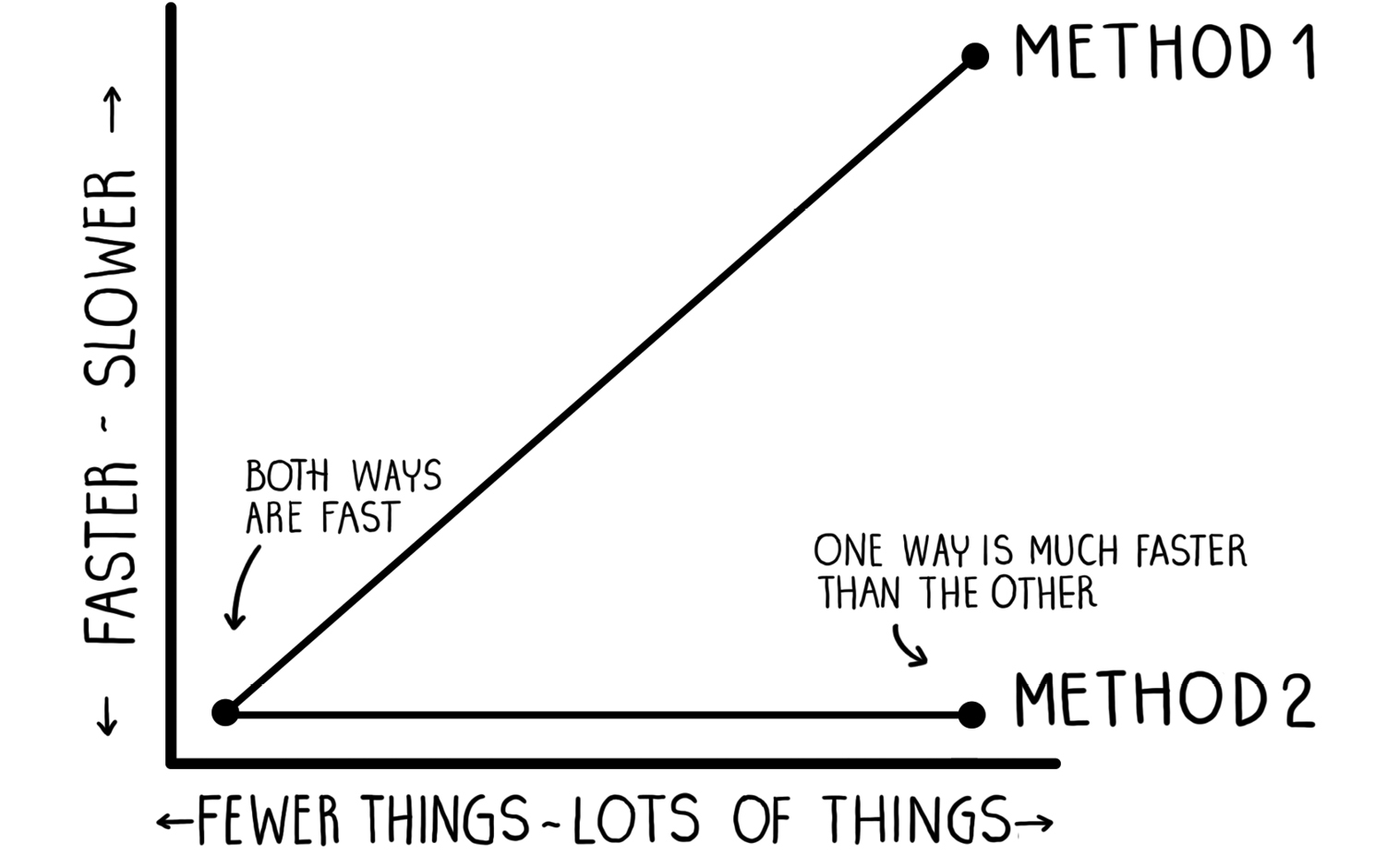
Those shapes of lines have names like linear and logarithmic, which we will flesh out and discuss throughout the book. And while both approaches are comparable in terms of performance when we have a few things, notice how that changes as the number of things increases. This book includes twelve familiar scenes, such as a living room, a tailor shop, and a department store. In each scene, there are a number of potential tasks to be done. After each illustration, a paragraph describes the scene, and a few pages of commentary and discussion relate the scene to concrete concepts from computer science and highlight at least two possible ways of undertaking the fundamental task at hand. One thats slower and one thats faster. That difference is what the books title aims to emphasize, albeit somewhat provocatively. The title is partly inspired by computer scientist Donald Knuths talk of good algorithms, which is to say fast or effective ones.