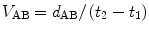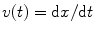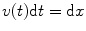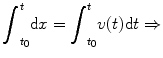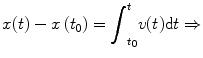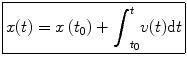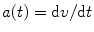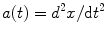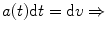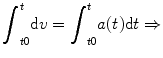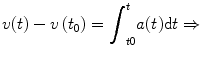Elefteriadou - An Introduction to Traffic Flow Theory

An Introduction to Traffic Flow Theory — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "An Introduction to Traffic Flow Theory" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...73

Part 1
Modeling Traffic: VehicleDriverDriving Environment Interactions

Lily Elefteriadou Springer Optimization and Its Applications An Introduction to Traffic Flow Theory 2014 10.1007/978-1-4614-8435-6 Springer Science+Business Media New York 2014

This first part of this book focuses on the movement of the basic unit of traffic, i.e., the single vehicle. This movement is a function of the fundamental equations of motion as well as the interactions between vehicle, driver, and environment (discussed in the Introduction and presented in Fig. 2). The principles presented in this part form the basis for understanding the performance of traffic streams and the principles of traffic flow theory.

Chapter presents the principles of the motion of a group of vehicles, i.e., car-following, lane-changing, and gap acceptance models. The chapter discusses primarily interactions between vehicles and also the effects of vehicle characteristics, driver characteristics, and driving environmental factors on these interactions.

Lily Elefteriadou Springer Optimization and Its Applications An Introduction to Traffic Flow Theory 2014 10.1007/978-1-4614-8435-6_1

Springer Science+Business Media New York 2014

1. Modeling the Motion of a Single Vehicle

Lily Elefteriadou 1

(1)

Department of Civil and Coastal Engineering, University of Florida, Gainesville, FL, USA

Abstract

The movement of a single vehicle can impact significantly the performance of a traffic stream. Consider a slow-moving vehicle at the front of a long line of vehicles traveling behind it, with no-passing opportunities. The performance of this lead vehicle significantly affects the speed and travel time of the following vehicles. Understanding the characteristics, performance, and movement of each vehicle type allows us to model groups of vehicles and to evaluate the performance of the traffic stream. Furthermore, the movement of individual vehicles allows us to develop better highway design and traffic control solutions. For example, understanding the acceleration and deceleration constraints of various vehicle types can help us design more effective passing zones and to allocate appropriate yellow and all-red intervals at signalized intersections.

The movement of a single vehicle can impact significantly the performance of a traffic stream. Consider a slow-moving vehicle at the front of a long line of vehicles traveling behind it, with no-passing opportunities. The performance of this lead vehicle significantly affects the speed and travel time of the following vehicles. Understanding the characteristics, performance, and movement of each vehicle type allows us to model groups of vehicles and to evaluate the performance of the traffic stream. Furthermore, the movement of individual vehicles allows us to develop better highway design and traffic control solutions. For example, understanding the acceleration and deceleration constraints of various vehicle types can help us design more effective passing zones and to allocate appropriate yellow and all-red intervals at signalized intersections.

This chapter first discusses the basic equations of motion for a single vehicle. The second part of the chapter discusses vehicle, driver, and environmental characteristics and their effects on vehicle motion.

Motion of a Single Vehicle

The motion of a single vehicle can be fully described mathematically using equations of motion. These are based on laws of physics and provide relationships between key parameters such as acceleration, speed, distance traveled, and travel time. This section derives and presents these equations of motion for various types of movement (constant speed, constant acceleration, and varying acceleration). The discussion in this section is based to a large degree on [].

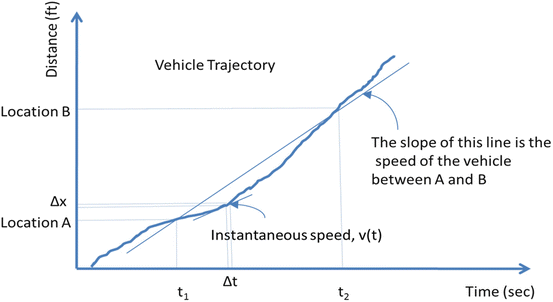
Figure presents a diagram with the trajectory of a vehicle, i.e., a plot providing the vehicles position as a function of time. The horizontal axis of the figure indicates the time, while the vertical axis indicates the respective location of the vehicle. This type of diagram is called a timespace diagram . The trajectory of the vehicle is the line connecting the locationtime points along the vehicles path. The average speed of the vehicle between locations A and B ( V AB) can be determined as follows:

Fig. 1.1

Trajectory of a vehicle

where d AB is the distance between points A and B (ft).

Visually, the average speed of the vehicle is determined by the slope of the line connecting the two points as shown in Fig. , the speed of the vehicle near location A is lower than the average speed between points A and B, as the slope of that line (labeled instantaneous speed) is smaller.

Mathematically, the instantaneous speed of the vehicle at time t , v ( t ), can be provided by:

where d x is the change in distance and d t the change in time.

The distance covered by the vehicle in time d t can be determined as:

By integrating both parts of this equation, we have:

(1.1)

This is the general equation for determining the distance traveled as a function of speed. Given any speed function, this equation can provide the distance traveled in time t , x ( t ).

The change in speed per unit of time is called acceleration ( a ). Mathematically, it is described as a function of speed as follows:

When the final speed of the vehicle is lower than its initial speed, the sign of d v is negative and the vehicle is decelerating. Throughout this book, we will be referring to both types of movements as acceleration, and we will be using acceleration functions.

Given the relationship between speed and distance provided above, acceleration can also be described as:

The speed function can be determined as follows:

Next page

1234567...73

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «An Introduction to Traffic Flow Theory»

Look at similar books to An Introduction to Traffic Flow Theory. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Marja-Liisa Siikonen

People Flow in Buildings

Michael W. Lucas

Network Flow Analysis

Bryan E. Porter

Handbook of Traffic Psychology

Jun Tanimoto

Fundamentals of Evolutionary Game Theory and its Applications

Lucas

Network Flow Analysis

Dorrance

Viscous hypersonic flow : theory of reacting and hypersonic boundary layers

Vlad

30 Powerful Ways To Drive Unlimited Traffic To Your Website: Traffic Powerhouse

Fortier

Theory/theatre : an introduction

Knowledge flow

Learning PHP and MySQL: by Knowledge flow

Knowledge flow

Java for Beginners: by Knowledge flow

Hassan M. Badr

Pumping Machinery Theory and Practice

Anthony Downs

Stuck in Traffic: Coping With Peak-Hour Traffic Congestion

Discussion, reviews of the book An Introduction to Traffic Flow Theory and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.