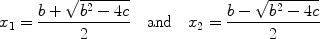Kamran Dadkhah Foundations of Mathematical and Computational Economics 10.1007/978-3-642-13748-8_1 Springer-Verlag Berlin Heidelberg 2011
1. Mathematics, Computation, and Economics
Abstract
Many believe that mathematics is one of the most beautiful creations of humankind, second only to music. The word creation , however, may be disputed. Have humans created something called mathematics? Then how is it that we increasingly discover that the world, and indeed the universe around us, obey one or another mathematical law? Perhaps to the faithful, the answer is clear: A higher power is the greatest mathematician of all. A worldly answer may be that humans discovered, rather than created, mathematics. Thus, wherever we look, we see mathematical laws at work. Whether humans created mathematics and it just so happened that the world seems to be mathematical, or the universe is a giant math problem and human beings are discovering it, we cannot deny that mathematics is extremely useful in every branch of science and technology, and even in everyday life. Without math, most likely we would be still living in caves. But what is mathematics? And why are so many afraid of it?
1.1 Mathematics
Many believe that mathematics is one of the most beautiful creations of humankind, second only to music. The word creation , however, may be disputed. Have humans created something called mathematics? Then how is it that we increasingly discover that the world, and indeed the universe around us, obey one or another mathematical law? Perhaps to the faithful, the answer is clear: A higher power is the greatest mathematician of all. A worldly answer may be that humans discovered, rather than created, mathematics. Thus, wherever we look, we see mathematical laws at work. Whether humans created mathematics and it just so happened that the world seems to be mathematical, or the universe is a giant math problem and human beings are discovering it, we cannot deny that mathematics is extremely useful in every branch of science and technology, and even in everyday life. Without math, most likely we would be still living in caves. But what is mathematics? And why are so many afraid of it?
To begin with, for the greatest part mathematics is nothing but logical thinking. Indeed, mathematics consists of three parts: definitions , logical thinking , and axioms . We will take up each of these parts in turn, but lets clear up one confusion right away: What about all those dreaded Greek and other strange symbols? First, we use Greek symbols because Greeks started the systematic study of mathematics and some reward must accrue to pioneers. Second, the Greek alphabet and symbols simply serve as a shorthand that makes understanding mathematics easier. If you dont believe this, consider how one of the great mathematicians of the Middle Ages, Omar Khayyam, explained the solution of a quadratic equation.
The second species. A square and a number equal a root . It is necessary in this class that the number should not be greater than the square of half the number of roots, otherwise the problem would be impossible to solve. If the number is equal to the square of half the root-number, then half the root-number is equal to the root of the square. If the number is less than the square of half the root, subtract it from the square of half the roots and extract the square root of the remainder, adding the result to half the roots or subtracting it from the latter. The sum, in case of addition, or the remainder, in case of subtraction, is the root of the square. The arithmetical proof of this theorem is known when its geometrical demonstration is known.
Translation, please! Put more clearly, the question is finding the solution of a quadratic equation of the form
The solution to this equation, which we shall discuss in , is
Khayyam argues that the equation does not have a solution if
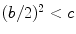
or
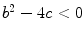
because this would result in a complex number and at the time complex numbers were not known. But if
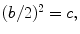
then
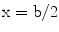
and if
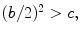
then the solutions are
Thus, Khayyam had correctly solved the problem, yet a modern reader would have difficulty understanding it. Nevertheless, if you think that 1000 years after Khayyam you can do better, then please write down a description of the problem and its solution in plain English. Clarity and economy require the use of symbols and conventions.
One other important lesson from the above quotation is that mathematics and symbols are two different things. Khayyam was doing mathematics; the fact that he did not use symbols made no difference. Symbols cannot make a banal statement about mathematics, and not using symbols cannot detract from the essence of a mathematical argument.
Going back to our discussion, the necessity of definitions should be clear. If we are to have a logical discussion, we should all speak the same language. In other words, an expression or statement should mean the same thing to all of us. A mathematical definition should be such that, in no uncertain terms, it includes all of the items that conform to the definition and excludes all that do not. In this matter, mathematicians are a bit obsessive-compulsive. They go to great lengths to make sure we are speaking about the same items and situations. But there are exceptions. In every branch of mathematics, a number of concepts are deemed too fundamental or basic to be defined. For example, in geometry, concepts such as point and line are at best vaguely defined. We assume that all are well aware of what we are talking about. The same is true about the concept of a set in set theory and a random event in probability theory. The rationale should be clear. Every concept has to be defined in terms of some other concept or object. We cannot start from nothing and expect to create a host of meaningful definitions. We may end up trying to define the meaning of the word word .
By far the largest part of mathematics is logical thinking, that is, starting with assumptions and deriving implications from them. In mathematics, every statement flows logically from another. As such, you do not get anything from math unless you have already put it in. It is like the work of a magician, who pulls a rabbit out of the hat as if it materialized out of thin air. But the rabbit was there all along, except that the audience could not see itperhaps because of distraction or you did not pay enough attention to see something that was in full view. Of course, let us not forget the skill of the magician. Not everyone can perform a magic trick like Houdini or Siegfreid and Roy.












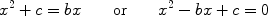
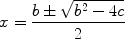
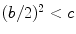 or
or 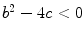 because this would result in a complex number and at the time complex numbers were not known. But if
because this would result in a complex number and at the time complex numbers were not known. But if 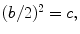 then
then 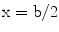 and if
and if 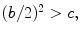 then the solutions are
then the solutions are