1. Introduction
The goal of the scientific discipline of particle physics is to understand the principles that govern the universe at its most fundamental level. The standard model of particle physics (SM) describes the current understanding of the elementary particles and the interactions among them, and represents the most accurate description of nature that we know today.
There are four known fundamental forces in nature, the electromagnetic, gravitational, weak and strong interactions. Each can be interpreted as resulting from the dynamics of a physical field, while the elementary particles can be understood as excited states of the corresponding fields. The fundamental (anti)matter particles are fermions, and consist of the (anti)leptons and (anti)quarks, while the interactions between the (anti)matter particles are mediated by the fundamental gauge bosons, so-called force carriers. The SM incorporates the particles and their interactions through the theoretical framework of the quantum field theory. However, there is no experimentally verified quantum theory of gravity, which is represented by a classical field within the general theory of relativity [], and is not part of the SM.
The basis for the SM was set with the gradual transformation of the classical understanding of electrodynamics into a relativistic quantum field theory named quantum electrodynamics (QED) in the 1940s, which was made possible after combining the revolutionary ideas of quantum mechanics and the special theory of relativity []. In the QED formulation, the massless spin-1 photon mediates the electromagnetic interaction between electrically charged particles.
Given the success of QED, efforts were started to understand the weak interaction, responsible for radioactive decays, by a similar, QED-inspired field theory. In the 1960s, these attempts culminated in a unified field theory for the electromagnetic and the weak interactions [] almost half a century later, confirming the proposed mechanism to be realized in nature.
Finally, the understanding of the strong interaction was accelerated by the introduction of the concept of quarks as the fundamental constituents of hadrons []. In this model, the strong interaction is mediated by massless spin-1 gluons between the quarks, which carry a color charge.
This completed the development of the SM, which can be regarded as a joint effort of theoreticians and experimentalists, as the main ideas were driven by both new theoretical developments as well as experimental discoveries. The description of particles and their interactions through the SM has been experimentally verified by many experiments over several decades with fantastic precision. Several particles and their properties have been predicted by the SM before they were discovered, giving further credence to the model.
Despite its impressive successes, the SM is not regarded as complete, and is thought to represent an intermediate step towards a more fundamental theory. The lack of reconcilability of the SM with general relativity is certainly one of its most profound shortcomings. Moreover, the SM has neither an explanation for dark matter, which contributes around 26% to the energy density of the observable universe [], which is thought to be responsible for the accelerated expansion of the universe. Furthermore, the SM has aesthetic problems: there is a large number of numerical constants which are not constrained by the SM itself. Also, the SM suffers from the so-called hierarchy problem, which emerges from the fact that gravity appears weaker than the other three interactions by many orders of magnitude, which leads to the necessity of fine-tuning of the models parameters, challenging its naturalness. Hence, huge past and ongoing efforts target the formulation and experimental verification of a more fundamental theory at higher energy scales that includes the SM in its low-energy limit.
Yet, the SM itself exhibits several problems that still remain to be solved. While the QED predictions are well understood and confirmed in an immensely precise manner, the strong interaction still poses many mysteries, which are yet to be understood. The research described in this document aims to contribute to this effort.
QCD describes the dynamics of the strong interaction in a self-consistent and compact way. However, concrete calculations can only be successfully performed in specific conditions. The level of the understanding of QCD processes is inevitably connected to the magnitude of the momentum transfer of the interacting particles (quarks and gluons), given the running strong coupling constant
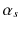
[], limiting the possibility to perform perturbative calculations as an expansion in orders of
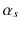
only for processes involving high momentum transfers at short distances (hard scattering), where
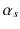
turns out to be small. At the other end of the energy scale, in the realm of soft QCD, characterized by processes involving small momentum transfers at long distances, the expansion breaks down, and perturbative calculations are no longer possible, limiting the predictive power of QCD in these conditions.
Processes leading to the formation of QCD bound states (hadronization) are difficult to access with QCD calculations, given that these processes are characterized by low momentum transfers [].
NRQCD is a QCD-inspired effective field theory, fully relying on the factorization between short-distance and long-distance effects. The NRQCD model describes quarkonium production as a superposition of the production of various pre-resonant
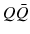
states, characterized by different spin, angular momentum and color eigenstates, including color-singlet (CS) and color-octet (CO) configurations. The long-distance effects, containing all non-perturbative physics involved, can be described by the so-called long-distance matrix elements (LDMEs), supposedly universal and constant parameters, determining the relative importance of the individual
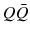
states with respect to the full quarkonium production cross section. The magnitude of the LDMEs can be estimated by NRQCD velocity scaling rules. The LDMEs of the individual intermediate
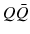
states are proportional to certain powers of the relative quark velocity v , which is rather small, given the heavy quark masses. Therefore, the non-perturbative hadronization process can be considered as an expansion in powers of v , limiting the number of contributing intermediate
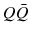
states, assuming a non-relativistic approximation []. The predictive power of NRQCD is limited given that the LDMEs are not calculable, and have to be determined from fits to experimental data. Several experimentally accessible physics observables are sensitive to the numerical values of the LDMEs and can therefore be used to perform their determinations by comparing theory calculations and data.













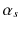 [], limiting the possibility to perform perturbative calculations as an expansion in orders of
[], limiting the possibility to perform perturbative calculations as an expansion in orders of 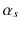 only for processes involving high momentum transfers at short distances (hard scattering), where
only for processes involving high momentum transfers at short distances (hard scattering), where 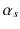 turns out to be small. At the other end of the energy scale, in the realm of soft QCD, characterized by processes involving small momentum transfers at long distances, the expansion breaks down, and perturbative calculations are no longer possible, limiting the predictive power of QCD in these conditions.
turns out to be small. At the other end of the energy scale, in the realm of soft QCD, characterized by processes involving small momentum transfers at long distances, the expansion breaks down, and perturbative calculations are no longer possible, limiting the predictive power of QCD in these conditions.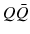 states, characterized by different spin, angular momentum and color eigenstates, including color-singlet (CS) and color-octet (CO) configurations. The long-distance effects, containing all non-perturbative physics involved, can be described by the so-called long-distance matrix elements (LDMEs), supposedly universal and constant parameters, determining the relative importance of the individual
states, characterized by different spin, angular momentum and color eigenstates, including color-singlet (CS) and color-octet (CO) configurations. The long-distance effects, containing all non-perturbative physics involved, can be described by the so-called long-distance matrix elements (LDMEs), supposedly universal and constant parameters, determining the relative importance of the individual 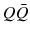 states with respect to the full quarkonium production cross section. The magnitude of the LDMEs can be estimated by NRQCD velocity scaling rules. The LDMEs of the individual intermediate
states with respect to the full quarkonium production cross section. The magnitude of the LDMEs can be estimated by NRQCD velocity scaling rules. The LDMEs of the individual intermediate 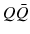 states are proportional to certain powers of the relative quark velocity v , which is rather small, given the heavy quark masses. Therefore, the non-perturbative hadronization process can be considered as an expansion in powers of v , limiting the number of contributing intermediate
states are proportional to certain powers of the relative quark velocity v , which is rather small, given the heavy quark masses. Therefore, the non-perturbative hadronization process can be considered as an expansion in powers of v , limiting the number of contributing intermediate 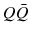 states, assuming a non-relativistic approximation []. The predictive power of NRQCD is limited given that the LDMEs are not calculable, and have to be determined from fits to experimental data. Several experimentally accessible physics observables are sensitive to the numerical values of the LDMEs and can therefore be used to perform their determinations by comparing theory calculations and data.
states, assuming a non-relativistic approximation []. The predictive power of NRQCD is limited given that the LDMEs are not calculable, and have to be determined from fits to experimental data. Several experimentally accessible physics observables are sensitive to the numerical values of the LDMEs and can therefore be used to perform their determinations by comparing theory calculations and data.