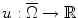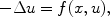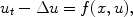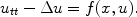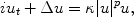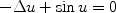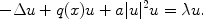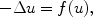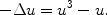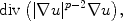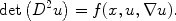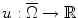Marino Badiale - Semilinear Elliptic Equations for Beginners Existence Results via the Variational Approach

Semilinear Elliptic Equations for Beginners Existence Results via the Variational Approach — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Semilinear Elliptic Equations for Beginners Existence Results via the Variational Approach" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...80

Marino Badiale and Enrico Serra Universitext Semilinear Elliptic Equations for Beginners Existence Results via the Variational Approach 10.1007/978-0-85729-227-8_1 Springer-Verlag London Limited 2011

1. Introduction and Basic Results

Marino Badiale 1

(1)

Dipartimento di Matematica, Universit di Torino, Torino, Italy

Marino Badiale (Corresponding author)

Email:

Enrico Serra

Email:

Abstract

The first chapter is an introduction. After a brief historical overview, we introduce the fundamental notions to be used later and the first simple existence results.

In particular we present a review of differential calculus for functionals, with many examples, and we introduce the fundamental notion of weak solution that allows one to interpret solutions of elliptic problems as critical points of functionals.

Convex functionals and their main properties are then described, providing the first examples of existence theorems.

Finally we recall the main results from the linear theory, particularly some spectral properties of elliptic operators that will be used throughout the book.

In this chapter, after a short historical overview, we introduce the fundamental notions to be used later and the first existence results, based on convexity arguments.

1.1 Motivations and Brief Historical Notes

Semilinear elliptic equations are the first nonlinear generalization of linear elliptic partial differential equations. It is well known that linear elliptic equations, like the ubiquitous Laplace and Poisson equations, represent models for wide classes of physical problems. This is the reason why they have been studied for more than two hundred years and continue to attract researchers even today. One example is that the solutions of the Laplace and Poisson equations can represent the stationary solutions (i.e. the state of a system when equilibrium is reached) of evolution equations of the utmost physical importance, such as heat and wave equations. Solutions of these equations also represent or describe the potential of force fields, in a variety of physical contexts, like electromagnetism, gravitation, fluid dynamics and so on.

It is also noted that the linear equations commonly used in mathematical physics are very often just a first approximation, valid within the range of certain assumptions, of more complex equations modelling phenomena of a nonlinear nature. Under slightly less restrictive assumptions one is frequently led from linear to semilinear equations, namely equations where the nonlinearity involves the unknown function, but not its derivatives. In addition, we recall that semilinear elliptic equations manifest themselves even in quantum physics, despite the fact that the fundamental structure of quantum physics is of a linear nature.

Some examples of semilinear elliptic equations include

representing the stationary states of nonlinear heat equations like

or nonlinear wave equations , such as

In all these examples u is the unknown, f is a (nonlinear) function, and is the Laplace operator.

In optics and in the theory of water waves one encounters the nonlinear Schrdinger equations ,

and again the stationary solutions solve the corresponding semilinear equation.

The elliptic sine-Gordon equation

appears in geometry, in the study of surfaces of constant negative curvature, and, again in geometry, important semilinear equations are related to classical problems, such as prescribing the scalar curvature on a manifold (the Yamabe problem ).

The theory of BoseEinstein condensates uses the time-independent GrossPitaevskii equation

The scalar field equations in classical or quantum physics are noteworthy; they have the form

for example

These are just a few examples of semilinear elliptic equations, which illustrate their frequent appearance in various areas of science.

The next step towards more complex nonlinear equations is given by quasilinear equations, where the nonlinear dependence involves not only the unknown function, but also all of its derivatives except those of the highest order. A very common class of quasilinear equations is given by the so-called p -Laplace equations, where the Laplacian is replaced by the operator

which reduces to the usual Laplacian when p =2.

The highest degree of nonlinearity is reached with fully nonlinear equations, in which the unknown function and all its derivatives are combined nonlinearly, as in the MongeAmpre equations

As a general principle, the more nonlinear the equation is, the more difficult it is.

In this book we concentrate on some types of semilinear elliptic equations, with some excursions into the realm of p -Laplace equations, confining ourselves to the cases where the theory developed for semilinear equations extends easily to the quasilinear context.

Of course elliptic equations can be studied with an astonishing variety of methods and techniques. In this book we present the variational approach, which is relatively simple, elegant and successful with large classes of problems.

Variational methods have a long history, which probably originated from the brachistochrone problem posed in 1696 and solved by Newton, Leibniz, Jakob and Johann Bernoulli, as well as de LHpital, although the problem of surfaces of revolution in a resisting medium studied by Newton dates back even further. Major contributions were also given by Euler, who published the first monograph on the Calculus of Variations in 1744, and by Lagrange who introduced formalisms and techniques essentially still in use today. The Maupertuis least action principle was another of the first variational frameworks to be set.

The classical example for the problems studied in this book is the Dirichlet Principle , namely the fact that the solution of a differential equation (of elliptic type) coupled with a boundary condition can be obtained as a minimizer of an appropriate functional. In one of the most classical cases, an open set in the plane or in the space is given, along with a real function f defined on the boundary of . The problem consists in finding a function

Next page

1234567...80

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Semilinear Elliptic Equations for Beginners Existence Results via the Variational Approach»

Look at similar books to Semilinear Elliptic Equations for Beginners Existence Results via the Variational Approach. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Tujin Kim

Equations of Motion for Incompressible Viscous Fluids: With Mixed Boundary Conditions

Shigeaki Koike

Nonlinear Partial Differential Equations for Future Applications: Sendai, Japan, July 10–28 and October 2–6, 2017

Ireneo Peral Alonso

Elliptic and Parabolic Equations Involving the Hardy-Leray Potential (de Gruyter Nonlinear Analysis and Applications)

Lauren Marino

Bookish Broads

Dazhong Lao

Fundamental Theories and Their Applications of the Calculus of Variations

Joseph H. Silverman

Rational Points on Elliptic Curves

Stanley J. Farlow

Partial Differential Equations for Scientists and Engineers

Constantin Corduneanu

Functional Differential Equations: Advances and Applications

Carroll

Abstract Methods in Partial Differential Equations

Cornelius Lanczos

The Variational Principles of Mechanics

Manuel Marino

An Integrated Approach to Wastewater Treatment: Deciding Where, When, and How Much to Invest (Directions in Development (Washington, D.C.).)

Lawrence C. Washington

Elliptic Curves: Number Theory and Cryptography

Discussion, reviews of the book Semilinear Elliptic Equations for Beginners Existence Results via the Variational Approach and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.