1. Geometry and Arithmetic
1.1 Rational Points on Conics
Everyone knows what a rational number is, a quotient of two integers. We call a point ( x , y ) in the plane a rational point if both of its coordinates are rational numbers. We call a line a rational line if the equation of the line can be written with rational numbers, that is, if it has an equation
with a , b , and c rational. Now it is pretty obvious that if you have two rational points, then the line through them is a rational line. And it is neither hard to guess nor hard to prove that if you have two rational lines, then the point where they intersect is a rational point. Equivalently, if you have two linear equations with rational numbers as coefficients and you solve them, you get rational numbers as answers.
The general subject of this book is rational points on curves, especially cubic curves. But as an introduction, we will start with conics. Let
be a conic. We will say that the conic is rational if the coefficients of its equation are rational numbers.
Now what about the intersection of a rational line with a rational conic? Will it be true that the points of intersection are rational? By writing down some example, it is easy to see that the answer is, in general, no. If you use analytic geometry to find the coordinates of these points, you will come out with a quadratic equation for the x -coordinates of the intersection points. And if the conic is rational and the line is rational, the quadratic equation will have rational coefficients. So the two points of intersection will be rational if and only if the roots of that quadratic equation are rational. But in general, they might be conjugate quadratic irrationalities.
However, if one of the intersection points is rational, then so is the other. This is true because if a quadratic polynomial
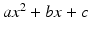
with rational coefficients has one rational root, then the other root is rational, because the sum of the roots is
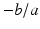
. This very simple idea enables one to completely describe the rational points on a conic. Given a rational conic, the first question is whether or not there are any rational points on it. We will return to this question later, and we suppose for now that we know of one rational point
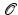
on our rational conic. Then we can get all of the rational points very simply. We just draw some rational line and project the conic onto the line from the point
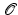
. (To project
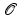
itself onto the line, we use the tangent line to the conic at
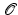
.)
A line meets a conic in two points, so for every point P on the conic we get a point Q on the line. Conversely, for every point Q on the line, by joining Q to the point
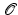
, we get a point P on the conic. (See Figure But now you see by the remarks that we have made that if the point P on the conic has rational coordinates, then the points Q on the line will have rational coordinates. And conversely, if Q is rational, then because
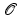
is assumed to be rational, the line through
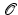
and Q is rational and meets the conic in two points, one of which is rational. So the other point is rational, too. Thus the rational points on the conic are in one-to-one correspondence with the rational points on the line. Of course, the rational points on the line are easily described in terms of rational values of some parameter.
Figure 1.1:
Projecting a conic onto a line
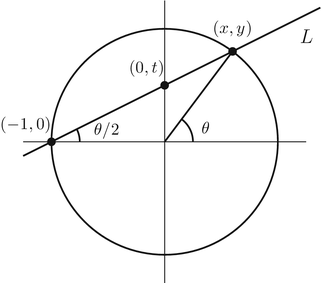
Lets carry out this procedure for the circle
We will project from the point (1,0) onto the y -axis. Lets call the intersection point (0, t ); see Figure . If we know x and y , then we can easily find t . The equation of the line L connecting (1,0) to (0, t ) is
The point ( x , y ) is assumed to be on the line L and also on the circle, so we get the relation
For a fixed value of t , this is a quadratic equation whose roots are the x -coordinates of the two intersections of the line L and the circle. Clearly
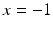
is a root, because the point (1,0) is on both L and the circle. To find the other root, we cancel a factor of 1 + x from both sides of the equation. This gives the linear equation
Solving this for x in terms of t , and then using the relation
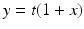
to find y , we obtain
Figure 1.2:
A rational parametrization of the circle
This is the familiar rational parametrization of the circle. And now the assertion made above is clear from these formulas. That is, if x and y are rational numbers, then
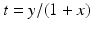
will be a rational number. And conversely, if t is a rational number, then it is obvious from the formulas () that the coordinates x and y are rational numbers. So this is the way that you get rational points on a circle, simply plug in an arbitrary rational number for t . That will give you all points except (1,0). (If you want to get (1,0), then you must substitute infinity for t !)













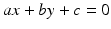
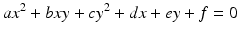
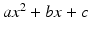 with rational coefficients has one rational root, then the other root is rational, because the sum of the roots is
with rational coefficients has one rational root, then the other root is rational, because the sum of the roots is 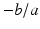 . This very simple idea enables one to completely describe the rational points on a conic. Given a rational conic, the first question is whether or not there are any rational points on it. We will return to this question later, and we suppose for now that we know of one rational point
. This very simple idea enables one to completely describe the rational points on a conic. Given a rational conic, the first question is whether or not there are any rational points on it. We will return to this question later, and we suppose for now that we know of one rational point 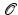 on our rational conic. Then we can get all of the rational points very simply. We just draw some rational line and project the conic onto the line from the point
on our rational conic. Then we can get all of the rational points very simply. We just draw some rational line and project the conic onto the line from the point 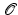 . (To project
. (To project 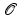 itself onto the line, we use the tangent line to the conic at
itself onto the line, we use the tangent line to the conic at 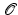 .)
.)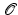 , we get a point P on the conic. (See Figure But now you see by the remarks that we have made that if the point P on the conic has rational coordinates, then the points Q on the line will have rational coordinates. And conversely, if Q is rational, then because
, we get a point P on the conic. (See Figure But now you see by the remarks that we have made that if the point P on the conic has rational coordinates, then the points Q on the line will have rational coordinates. And conversely, if Q is rational, then because 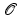 is assumed to be rational, the line through
is assumed to be rational, the line through 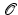 and Q is rational and meets the conic in two points, one of which is rational. So the other point is rational, too. Thus the rational points on the conic are in one-to-one correspondence with the rational points on the line. Of course, the rational points on the line are easily described in terms of rational values of some parameter.
and Q is rational and meets the conic in two points, one of which is rational. So the other point is rational, too. Thus the rational points on the conic are in one-to-one correspondence with the rational points on the line. Of course, the rational points on the line are easily described in terms of rational values of some parameter. 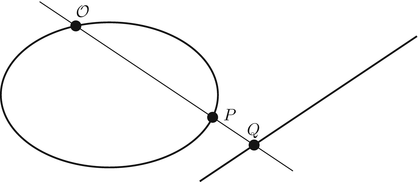
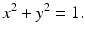
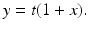
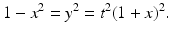
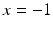 is a root, because the point (1,0) is on both L and the circle. To find the other root, we cancel a factor of 1 + x from both sides of the equation. This gives the linear equation
is a root, because the point (1,0) is on both L and the circle. To find the other root, we cancel a factor of 1 + x from both sides of the equation. This gives the linear equation 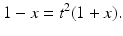
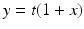 to find y , we obtain
to find y , we obtain 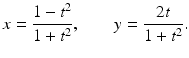
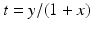 will be a rational number. And conversely, if t is a rational number, then it is obvious from the formulas () that the coordinates x and y are rational numbers. So this is the way that you get rational points on a circle, simply plug in an arbitrary rational number for t . That will give you all points except (1,0). (If you want to get (1,0), then you must substitute infinity for t !)
will be a rational number. And conversely, if t is a rational number, then it is obvious from the formulas () that the coordinates x and y are rational numbers. So this is the way that you get rational points on a circle, simply plug in an arbitrary rational number for t . That will give you all points except (1,0). (If you want to get (1,0), then you must substitute infinity for t !)