Chris Mortensen - The Impossible Arises: Oscar Reutersvärd and His Contemporaries

Contents

The Impossible Arises

SPECIAL PUBLICATIONS OF THE LILLY LIBRARY

The Impossible Arises

OSCAR REUTERSVRD

AND HIS CONTEMPORARIES

Chris Mortensen

INDIANA UNIVERSITY PRESS

This book is a publication of

Indiana University Press

Office of Scholarly Publishing

Herman B Wells Library 350

1320 East 10th Street

Bloomington, Indiana 47405 USA

iupress.indiana.edu

2022 by Chris Mortensen

All rights reserved

No part of this book may be reproduced or utilized in any form or by any means, electronic or mechanical, including photocopying and recording, or by any information storage and retrieval system, without permission in writing from the publisher. The paper used in this publication meets the minimum requirements of the American National Standardfor Information SciencesPermanence of Paper for Printed Library Materials, ANSI Z39.48-1992.

Manufactured in the United States of America

First Printing 2022

Cataloging information is available from the Library of Congress.

ISBN 978-0-253-06233-8 (cloth)

ISBN 978-0-253-06234-5 (e-book)

Dedicated to Bruno Ernst and Steve Leishman: Staunch Impossibilists Both

| CONTENTS

M any people are aware of the genre of art known to its practitioners as impossible figures. To describe this as art is already interesting, since its very existence brings forth the question of whether instead it is somewhere midway between art and scienceor between art and mathematics, especially geometry.

There are several widespread misunderstandings about our subject matter. One concerns the originators of the Impossible Figures movement (called IF for short by its practitioners). It is commonly believed that the originators were the great Dutch graphic artist M. C. Escher and his collaborators Lionel and Roger Penrose. This book aims to set the record straight, by showing that the Swedish artist and art historian Oscar Reutersvrd made his discovery of impossible figures over twenty years earlier than Escher did, while at the same time being eighteen years the younger in age. This is not to diminish Eschers contribution: as will become clear, I hold Eschers work in the highest esteem. But Reutersvrd got there first.

I also want to clarify other misunderstandings that are of a more philosophical sort. Perhaps the most significant is the tendency to describe impossible figures as illusions. This terminology is almost ubiquitous, even among artists of impossibilia themselves. One of our jobs is therefore to clarify this mistake. The mistake is important because, as we see, it implies that contradictory visual contents arise solely from a kind of misperception of real objects in the world. While it is true, and important, that contradictory contents can arise this way, it is not the only way, nor even the first way: rather, the originators of IF were using their imaginations. This leads to what is perhaps the main philosophical message of the book: namely, that the human imagination escapes not only the possible, but even the logically consistent; that humans play with contradictory concepts without intellectual collapse. We will be seeing this in due course.

This book is therefore a mixture of philosophy and analytical writing in art history. It is, I trust, fit for the lecture room but also for the coffee table.

To show Reutersvrds contributions, I make use of an extensive archive purchased in 2014 by Indiana University from Bruno Ernst, who was a student and close associate of both Reutersvrd and Escher. This archive consists of some 1,773 letters and drawings, mostly by Reutersvrd, which he sent to Ernst. Indiana University and President McRobbie are to be congratulated for the vision they have shown in making this purchase, and they are to be thanked for facilitating the project. Research for this book was funded by a grant from the Australian Research Council 20142016. , Impossible Possibilities Exhausted by Richard Pybus, published in Konstperspektiv 1.87 (1987) and, from the same journal, the reply No Witness to the Truth by Oscar Reutersvrd.

I wish to thank the following institutions and individuals for assisting with the provision of images and permission to reproduce: the Lilly Library of Indiana University; the National Gallery of Art, Washington, DC; the Josef and Anni Albers Foundation; Carlo del Prete, from the estate of Sandro del Prete; Istvn Orosz; Pontus Reutersvrd; Bruno Ernst; Wiley Global Permissions; and the Australian Copyright Council. Thanks to Douglas Hofstadter for a timely intervention on copyright.

Finally, I especially wish to thank Steve Leishman and Peter Quigley for their assistance with the Impossible Figures project and earlier projects on the theory of inconsistency; and to thank my wife Catherine Speck for bringing to bear her skills as an art historian, an archivist, and the author of .

It is with great sadness that I must record here Steve Leishmans death: his sense of humor helped to keep us all sane enough to complete the project.

CM, The University of Adelaide, March 2021

The Impossible Arises

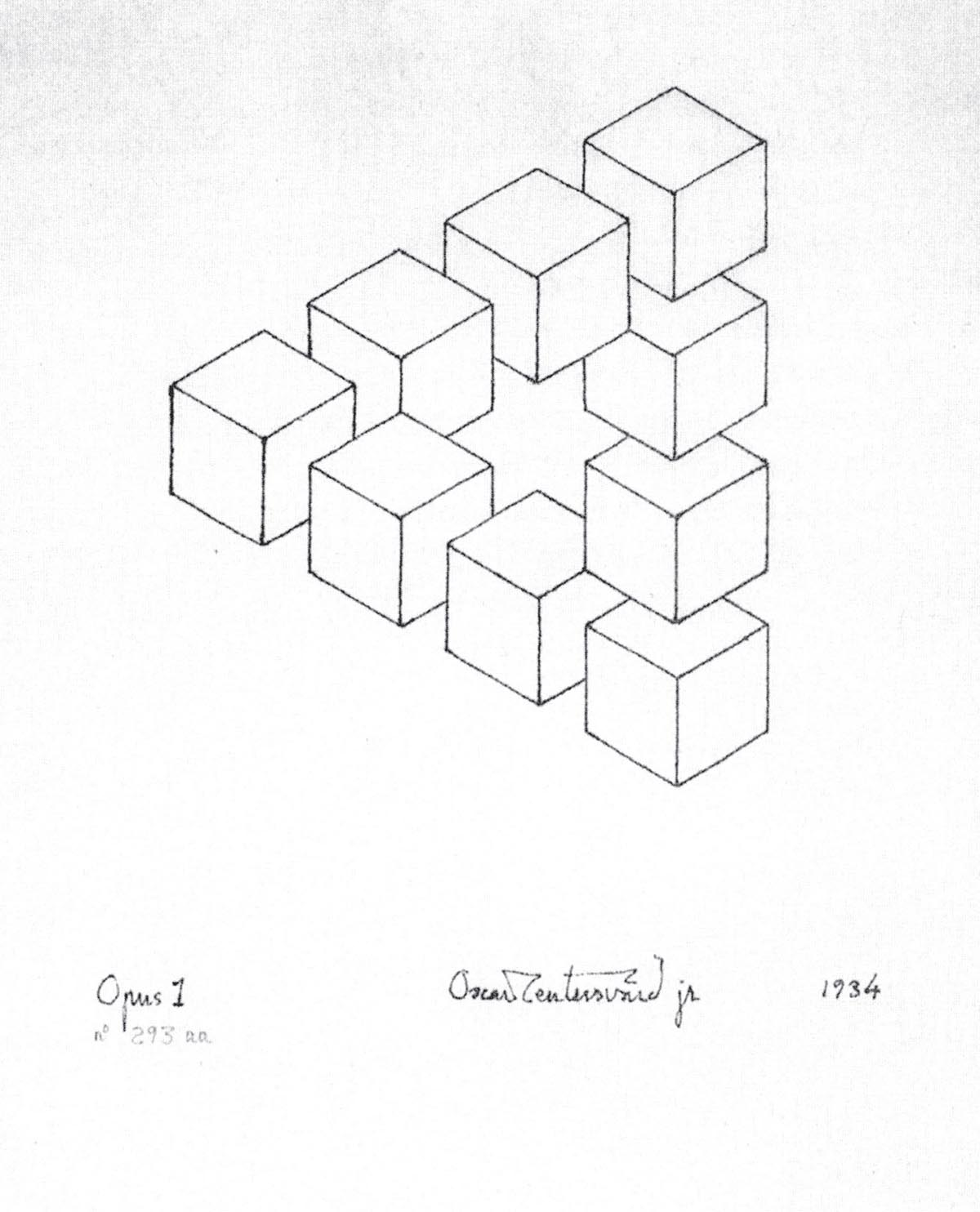
FIGURE 1.1. Opus 1, the Triangle, 1934

O ne day in 1934 in Stockholm, young Oscar Reutersvrd, aged eighteen years, sat bored in his high school Latin class. He drew what you see in .

Now, if we think of this as representing a three-dimensional figure, in the way we do with perspective, then when we move from cube 1 to cube 2 the figure turns in, turning away from you, the viewer. Cube 1 partly obscures cube 2; hence, cube 1 is closer to you than cube 2. That is, cube 1 is closer as judged along a normal or perpendicular to the page. By a similar observation, cube 2 is closer than cube 3. This observation can be repeated all the way around the figure, until we eventually observe that cube 9 is closer than cube 1. But of course, if any three things have the property that one is closer than a second and the second is closer than a third, then it must be that the first is closer than the third. (This property is technically known as the transitivity of the relation closer than). If you apply the transitivity property several times, going clockwise around our figure, it follows that cube 1 is closer to you than cube 1 itself. But that is absurd, a contradiction: surely it is a matter of logic or mathematics that nothing can be closer than itself!

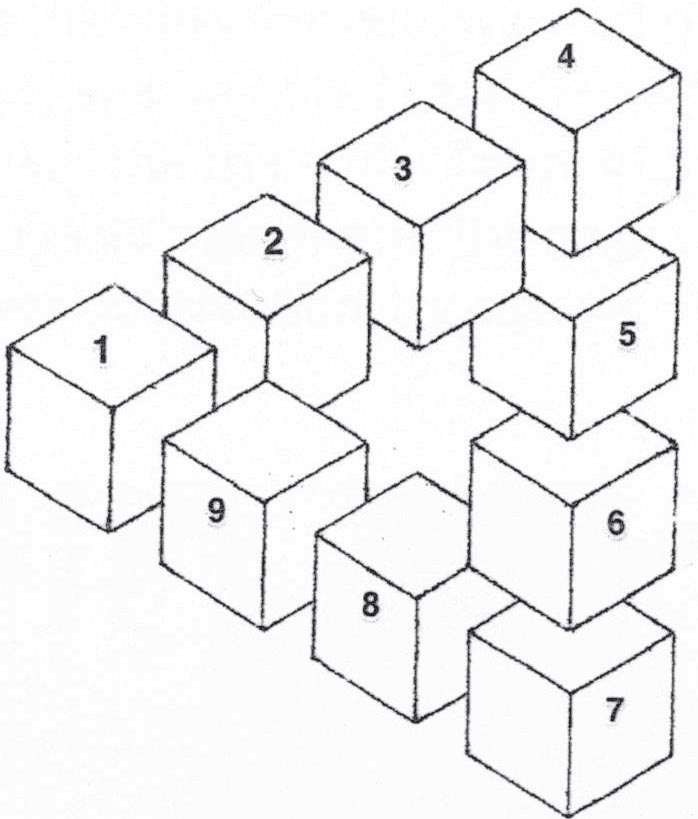
FIGURE 1.2. Opus 1 with numbers

The details of this argument might be challenged. For example, we might want to say that cubes 47 are equidistant from the viewer, though even in that case the argument for impossibility goes through much as before. That is to say, it seems that some such argument must be at the bottom of the common judgment that Opus 1, considered as representing a three-dimensional figure, depicts an impossibility. And yet how can one draw an impossibility, something that cannot exist?

Oscar had the wits to think that he might have come across something special. Just how special it was, we will see as we go along. He asked his school friend Jan Cornell, who was keen on mathematics, whether he had seen anything like it in mathematics books. Jan suggested that Oscar look for it in the library. But he had no success; it was an original. Jan himself could see the impossibility of the figure, but he thought of a different argument for its impossibility. He saw that the three angles of the triangle, formed by the outside edges of cubes 1, 4, and 7, were all right angles, whose sum was therefore 270 degrees; and he noted that the angles of a triangle add up to 180 degrees, which makes the triangular figure impossible. He called it non-Euclidean, since in Euclids geometry the angles of a triangle add up to 180 degrees. This is a clever observation, though we will see later that it is less than conclusive.