Alfred S. Posamentier - The Mathematics of Everyday Life

A book of this complexity requires very capable editorial management and copyediting. We wish to thank Catherine Roberts-Abel for very capably managing the production of this book, and offer very special thanks to Jade Zora Scibilia for truly outstanding editing throughout the various phases of production. We also thank Hanna Etu for her support, which was also much appreciated. The editor in chief of Prometheus Books, Steven L Mitchell, deserves praise for enabling us to approach the general readership to expose the mathematical wonders that help explain our everyday experiences. Christian Spreitzer would like to thank Dr. Katharina Brazda for contributing ideas and for her support during the writing of this book.

As we begin our exploration of the many obvious, and less obvious, occurrences of mathematics in our daily experiences, it would only be fitting that we begin with some of the historical highlights of where our mathematical usage began. It is well-known that the earliest uses of mathematics were portrayed with symbols of different kinds than what is used today. Best known is the use of hieroglyphics in the ancient Egyptian world. We still see today many applications of roman numeralson cornerstones of buildings, on some clock or wristwatch faces, some preliminary book pages, and so on. Yet the most common use of symbols is the set of the 10 digits we use to represent numbers in the base-10, which originated in India. Let's first consider the origin of numbers so that we can better appreciate those that we use today.

THE ORIGIN OF OUR NUMBER SYMBOLS

Concepts for the numbers 1, 2, 3, 4, 5, 6, 7,can be traced back to the origins of human history. Representations of these numbers must have arisen naturally as soon as humans started to count objects, animals, ). They are still used today for counting or tallying the score in a game.

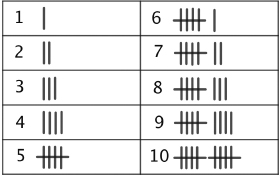
Figure 1.1.

Since the representation of any number is obtained from that of its predecessor by simply adding one mark, tally marks are very convenient for documenting ongoing results. Historically, they constitute the origin of all numeral systems, and their usage dates back to the Upper Paleolithic age (roughly 50,000 to 10,000 BCE). References to tally marks can also be found in much more sophisticated numeral systems of ancient cultures, and the Japanese symbols for 1, 2, and 3 bear this resemblance still today (see ).

Figure 1.2. (From left to right) Ancient Egyptian; Babylonian; Ancient Indian; Roman; and Japanese numeral systems.

The introduction of numerals for the quantities represented by 1,2,3,4,5,6,7,is an almost inevitable consequence of the act of counting. We then could say that the positive integers were not developed or invented; rather, they were discovered. The German mathematician Leopold Kronecker (18231891) is often quoted with the phrase, God made the natural numbers; all else is the work of man. Here, the term natural number, referring to an element of the set N={1, 2, 3,}, was introduced in 1888 by the German mathematician Richard Dedekind (18311916).

THE MOST IMPORTANT NUMBER IN MATHEMATICS

The first number that was truly invented by the human mind is the number zero, 0. Many mathematicians would regard zero as the most important number in mathematics, since a number system without a notation for zero is extremely impractical for dealing with very small or very large numbers. Just imagine how to represent one million or one thousandth as a decimal number without having a symbol for the concept of zero.

The development of a place-value system by the Babylonians in ancient Mesopotamia in the second millennium BCE was one of the first historical highpoints of mathematics. In a place-value system, the exact position of a digit within a number is relevant for the value it represents. The Babylonians had no concept or notation for zero, which caused difficulties for many-digit numbers and resulted in severe notational problems. Since their numeral system was a sexagesimal system (base-60), a Babylonian three-digit number D2D1D0 would represent the number D2 602 + D1 601 + D0 600 in the decimal system, but the notational problems that arise when there is no zero digit are essentially the same for all place-value systems. To demonstrate these notational problems, we will consider familiar decimal numbers rather than the Babylonian sexagesimal numbers. If there is no digit 0, how can we, for example, distinguish the number 2018 from 218? The Babylonians indicated the absence of a certain positional value by a space between sexagesimal numerals. This would correspond to writing 2 18 for the number 2018. Clearly, this practice becomes quite problematic when two or more consecutive positions need to be left out, as in the number 1001. Moreover, using spaces for empty positions does not resolve all ambiguities, since we can hardly add a space at the end of a number. Indeed, the Babylonians used identical representations for 1, 60, and 602, which would correspond to writing just 1 for the numbers 1, 10, 100, or any other power of 10. The number that was actually intended always had to be inferred from the context. Around 300 BCE, the Babylonians introduced a placeholder symbol for empty positions, making the notation less ambiguous. Yet this symbol was never used at the end of a number, so the written numbers 1, 60, and 602 still could not be distinguished from one another without knowing the context.

Babylonian clay tablets dating from the second millennium BCE already cover calculations with fractions, algebra, quadratic and cubic equations, and the Pythagorean theoremmore than a thousand years before Pythagoras was born. It might appear strange to us that one of the most mathematically advanced civilizations of their time never developed a concept of zero, especially when we think about the associated notational difficulties the Babylonians had to deal with.

Who invented the zero, then? It is documented that the Greco-Egyptian mathematician and philosopher Claudius Ptolemy (ca. 100ca. 170) used a symbol for zero within a sexagesimal numeral system in his astronomical writings. (More about Fibonacci in the next section.)

The introduction of zero into the decimal system dramatically simplified calculations with large numbers, thereby making mathematics, in general, a much more practicable and powerful tool. It surely was the most significant step in the development of a number system, and it laid the basis for many great advances in commerce, navigation, astronomy, physics, and engineering. Inventing a notion of zero, and raising this symbol for nothing to a number on its own right, requires a considerable mental abstraction that should be ranked among the greatest achievements of the human mind in the ancient world.

THE FAMOUS FIBONACCI NUMBERS

Now that we have established the beginnings of the number zero, let's see how the numbers that we use today evolved and spread throughout the world. As mentioned above, they originated in Indiainvented there by mathematicians between the first and fourth centuries CEand were brought into the European world in the year 1202 by the famous mathematician Leonardo of Pisa, better known today as Fibonacci. As mentioned above, Fibonacci wrote a book called