

Copyright 2015 by SAGE Publications, Inc.
All rights reserved. No part of this book may be reproduced or utilized in any form or by any means, electronic or mechanical, including photocopying, recording, or by any information storage and retrieval system, without permission in writing from the publisher.
Printed in the United States of America
Library of Congress Cataloging-in-Publication Data
Hunter, John E. (John Edward), 19392002.
Methods of meta-analysis: correcting error and bias in research findings / Frank L. Schmidt, University of Iowa, John E. Hunter, Michigan State University. Third edition.
pages cm
Includes bibliographical references and index.
ISBN 978-1-4522-8689-1 (hardcover : alk. paper)
1. Social sciencesStatistical methods. 2. Meta-analysis. I. Schmidt, Frank L. II. Title.
HA29.H847 2015
300.72dc23 2013039086
This book is printed on acid-free paper.
14 15 16 17 18 10 9 8 7 6 5 4 3 2 1

FOR INFORMATION:
SAGE Publications, Inc.
2455 Teller Road
Thousand Oaks, California 91320
E-mail:
SAGE Publications Ltd.
1 Olivers Yard
55 City Road
London EC1Y 1SP
United Kingdom
SAGE Publications India Pvt. Ltd.
B 1/I 1 Mohan Cooperative Industrial Area
Mathura Road, New Delhi 110 044
India
SAGE Publications Asia-Pacific Pte. Ltd.
3 Church Street
#10-04 Samsung Hub
Singapore 049483
Acquisitions Editor: Vicki Knight,
Editorial Assistant: Jessica Miller
Digital Content Editor: Katie Guarino
Production Editor: Laura Barrett
Copy Editor: Gillian Dickens
Typesetter: C&M Digitals (P) Ltd.
Proofreader: Wendy Jo Dymond
Indexer: Will Ragsdale
Cover Designer: Candice Harman
Marketing Manager: Nicole Elliott
Brief Contents
Detailed Contents
List of Tables
List of Figures
Preface
Overview of the Third Edition
Meta-analysis is today even more important to the research enterprise than it was when the last edition of this book appeared in 2004 (a fact that is fully explored in ). One reason for this is that meta-analysis is increasingly providing the foundation for evidence-based professional practice in a wide variety of fields, ranging from human resource management to medicine. In recent years, there have been important new methodological developments in meta-analysis, and these are addressed in this book. This book has been prepared to be more user-friendly than the previous editions. Many detailed derivations of equations for which proof no longer need be presented have been eliminated (with references given to sources where they can be found by those interested). In addition, a great deal of effort has been put into making the language of this book as clear as possible to all readers regardless of their statistical and psychometric backgrounds.
Certain new topics appear in multiple chapters throughout the book. For example, there is an expanded treatment of confidence intervals (CIs) in meta-analysis in , CIs are computed for mean observed and corrected effect sizes, along with CrIs. Discussions of the proper interpretation of the percentage or proportion of variance accounted for in meta-analysis are found in these same chapters. The key point is that the square root of the proportion of variance is the correlation between statistical and measurement artifacts and the observed correlations or d values and that this statistic is more informative than the proportion of variance accounted for.
Many improvements have been made in the package of meta-analysis programs available for applying the methods presented in this book. Some examples include the following. It is now possible to import data files from Excel. All programs now provide CIs around mean observed and corrected effect sizes, as well as CrIs. New features now make it easier to run meta-analyses when there is no range restriction. The upper limit on the number of studies in a meta-analysis has been raised to 1,000. A method of detecting and correcting publication bias (cumulative meta-analysis) has been added. A full list of program improvements can be found in the Appendix to this book. Throughout this book, the example meta-analyses presented are now calculated using the programs in this package.
It is appropriate to point out that the presentations in the book do not rigidly follow statistical conventions. For example, 2 might appear without the circumflex that indicates that it is not the actual population value but rather an estimate of that value (i.e., 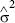 ). We use statistical symbols in this manner for convenience, and in all cases, the context and the text makes it clear which symbols stand for estimates and which stand for actual population parameters. We are aware that our usage of symbols causes some statisticians to tear their hair out.
). We use statistical symbols in this manner for convenience, and in all cases, the context and the text makes it clear which symbols stand for estimates and which stand for actual population parameters. We are aware that our usage of symbols causes some statisticians to tear their hair out.
There have been important improvements and additions in individual chapters. Here we summarize only the major changes. Corrections for measurement error are critical in meta-analysis, but there is often confusion as to the appropriate type of reliability coefficient to use. To address this, now contains an expanded and more complete treatment of this question to guide users.
are now calculated with the programs for this method. The long technical derivation of the multiplicative method, which has proved to be less accurate, has been dropped. Also, there is now a much clearer presentation of methods for conducting a mixed meta-analysisone in which one artifact is corrected individually in each study while the other artifacts are corrected based on artifact distributions. This presentation is accompanied by a detailed worked numerical example.
In , only minimal changes have been necessary.
now contains an improved presentation of methods for conducting meta-analysis of d values when artifacts beyond sampling error and measurement error in the dependent variable measure are corrected for. There is a clear explanation of how to convert d values to point-biserial correlations, conduct the meta-analysis in the r statistic metric, and then convert the meta-analysis results back into the d statistic metric. This approach to meta-analysis of d values has become increasingly common in the literature.
now presents the needed equations for computing the appropriate d values from these designs and the equations for the sampling error variance of the resulting d values. These methods allow d values from these experimental designs to be included in the meta-analysis along with the d values from the independent groups design. An equation is also presented for adjusting the sample sizes of the different designs, so that the d value and the adjusted N can be entered into the meta-analysis programs written for the independent groups design studies. This step ensures that the sampling error variances computed by the programs are correct.
.) In connection with confidence intervals, there is an explanation of the differences in how these are computed in the Hunter-Schmidt and the Hedges-Vevea meta-analysis methods. Finally, there is a discussion of the use of the odds ratio statistic in psychology and social science research.
Next page











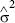 ). We use statistical symbols in this manner for convenience, and in all cases, the context and the text makes it clear which symbols stand for estimates and which stand for actual population parameters. We are aware that our usage of symbols causes some statisticians to tear their hair out.
). We use statistical symbols in this manner for convenience, and in all cases, the context and the text makes it clear which symbols stand for estimates and which stand for actual population parameters. We are aware that our usage of symbols causes some statisticians to tear their hair out.