K. Dane Wittrup - Quantitative Fundamentals of Molecular and Cellular Bioengineering

The universe is full of magical things patiently waiting for our wits to grow sharper.

Eden Phillpotts

Living systems are not static. Cells grow and divide; signals propagate over space and time; organisms are born, develop, grow, age, and die. This constant change is driven by networks of time-varying chemical transformations, macromolecular binding events, and changes in subcellular localization that combine to create complex functional behaviors. Evolution shapes the functions of molecules, the properties of cells, the characteristics of organisms, and the very existence of species. These dynamic rate processes propel biology at all length and time scales, from single molecules to worldwide ecosystems, from picoseconds to eons. In this text, we examine these rate processes and develop a quantitative toolkit useful for studying and engineering biological systems.

Many of the intellectual underpinnings for these approaches were originally developed in the discipline of chemical engineering, wherein understanding the networks of reactions forming and breaking covalent bonds was essential to the design and operation of petrochemical plants. Analogously, individual noncovalent binding events are the underlying building blocks of most biological functions. An understanding of these events is central to developing a quantitative and predictive description of any biological system. Those individuals with an engineering mindset are often best motivated by understanding the real-world applications of a body of knowledge. With that goal in mind, lets first take a look at some biological systems where dynamic rate processes drive overall outcomes.

Example 1-1BiosensorsPerhaps the most basic example consists of measuring the rate and extent of complex formation between two noncovalent binding partners, as shown in . Despite the apparent simplicity of this single binding and dissociation event, a surprising variety of complications can arise in performing and interpreting experiments with this type of device. A mathematical description is an essential tool for navigating toward a fuller understanding of the binding event being measured. We will consider biosensors in greater detail in chapter 3 (as well as in case study 8-4 in chapter 8).

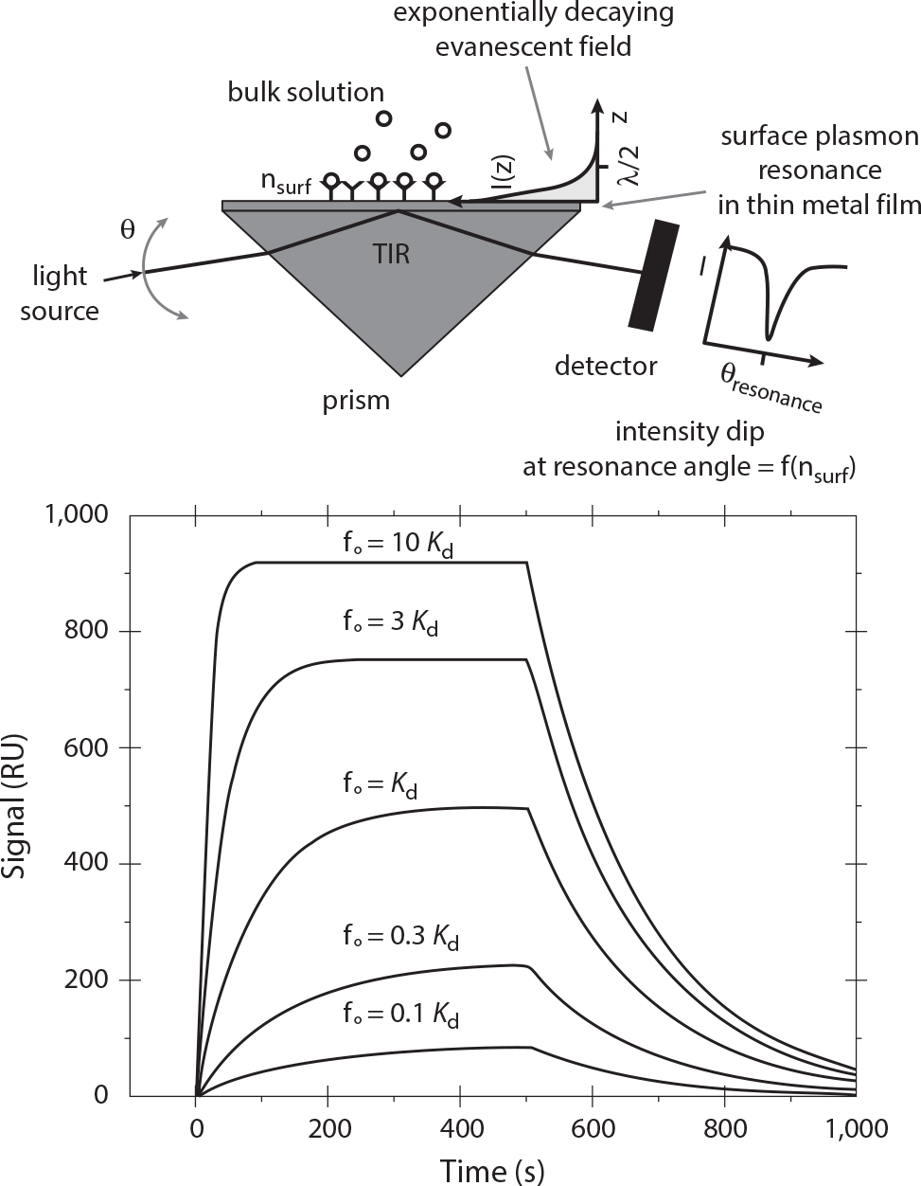
Schematic diagram and example data from a biosensor that detects complex formation via a phenomenon called surface plasmon resonance. The device shown at the top of the figure measures in real time (using optics from below the film) the extent of binding of soluble ligand at concentration f (small circles) to surface-immobilized protein (Y-shaped objects). The curves in the lower figure indicate how formation of macromolecular complexes on the sensor surface increases the devices signal readout as a function of time. Once free ligand is washed away continuously starting at 500 seconds, the signal decreases. Extracting quantitative information about the rate of formation and dissociation of the complex requires formulation of a mathematical description of the binding process [1] . TIR = total internal reflection.

Example 1-2Gene expressionThe dynamics of gene expression and the sensitivities of each genes expression to changing environmental conditions are of fundamental importance in cell function and engineering. The process of expressing a given gene is the sum total of many binding and chemical transformation events: from transcription factors binding DNA to the machinelike complexity of ribosomal translation of an mRNA molecule into a polypeptide. A quantitative description of the time-varying dynamics of gene expression can be essential to understanding or engineering its behavior. In , one level of quantitative description is represented. We will discuss the fundamental analysis of enzymatic processes in chapter 4 and return to gene expression models in chapter 5 (with additional considerations on stochasticity in chapter 9).

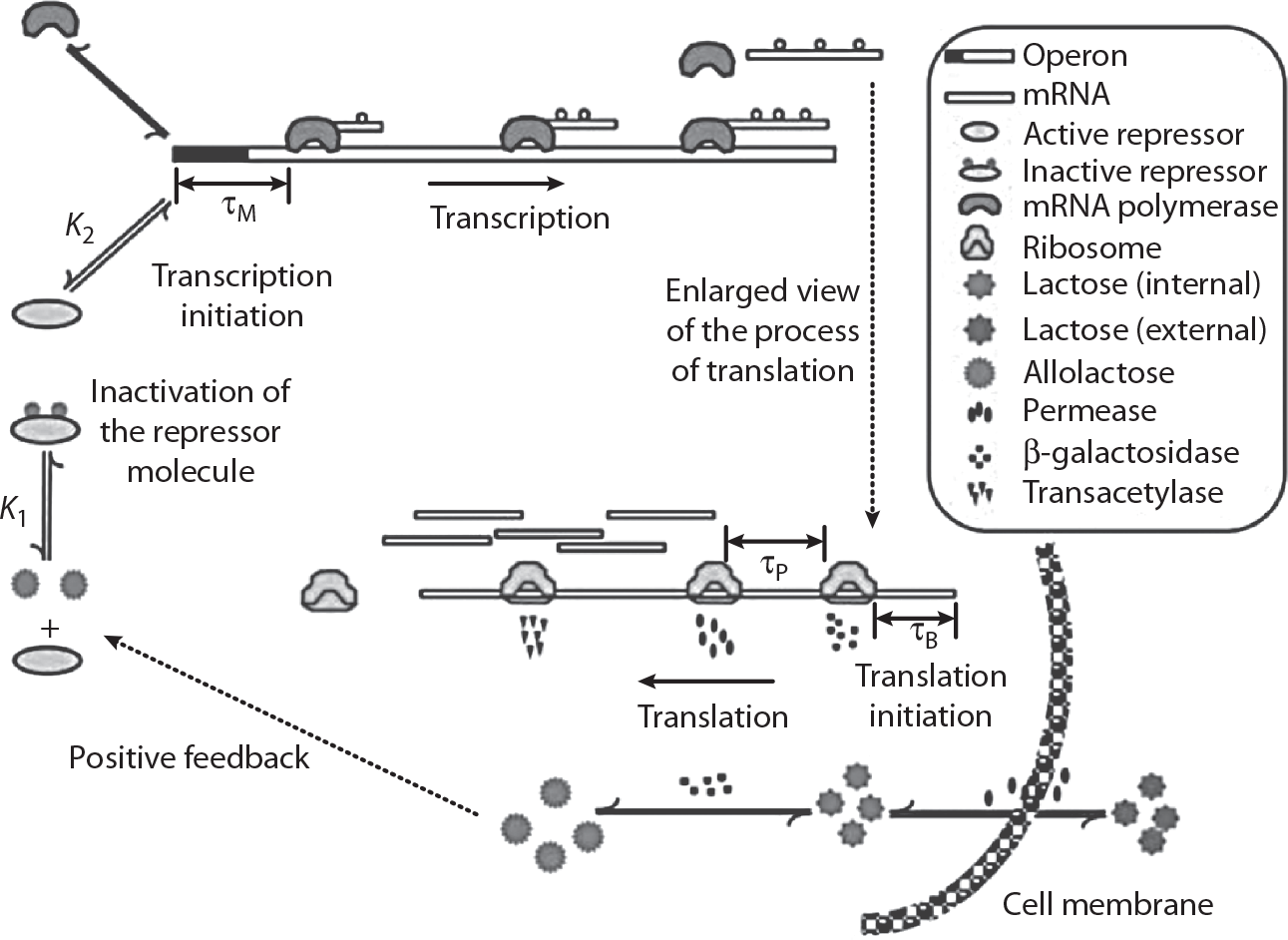
A simplified mechanistic description of the rate processes involved in gene expression. Such models can be useful for understanding the steady-state and dynamic variation in the levels of a gene product as a function of system inputs, such as lactose concentration [2] .

In , the behavior of a synthetic switchlike gene network is shown, in which the transient presence of specific inducer molecules alters the pattern of genes expressed until different inducer molecules are transiently applied. Network dynamics are the focus of chapter 6. This particular construct (further examined in chapter 9) inspired legions of biological engineers to work in the field of synthetic biology, wherein a designed genetic construct might be translated to a predictable, reliable, robust, and useful biological behavior.

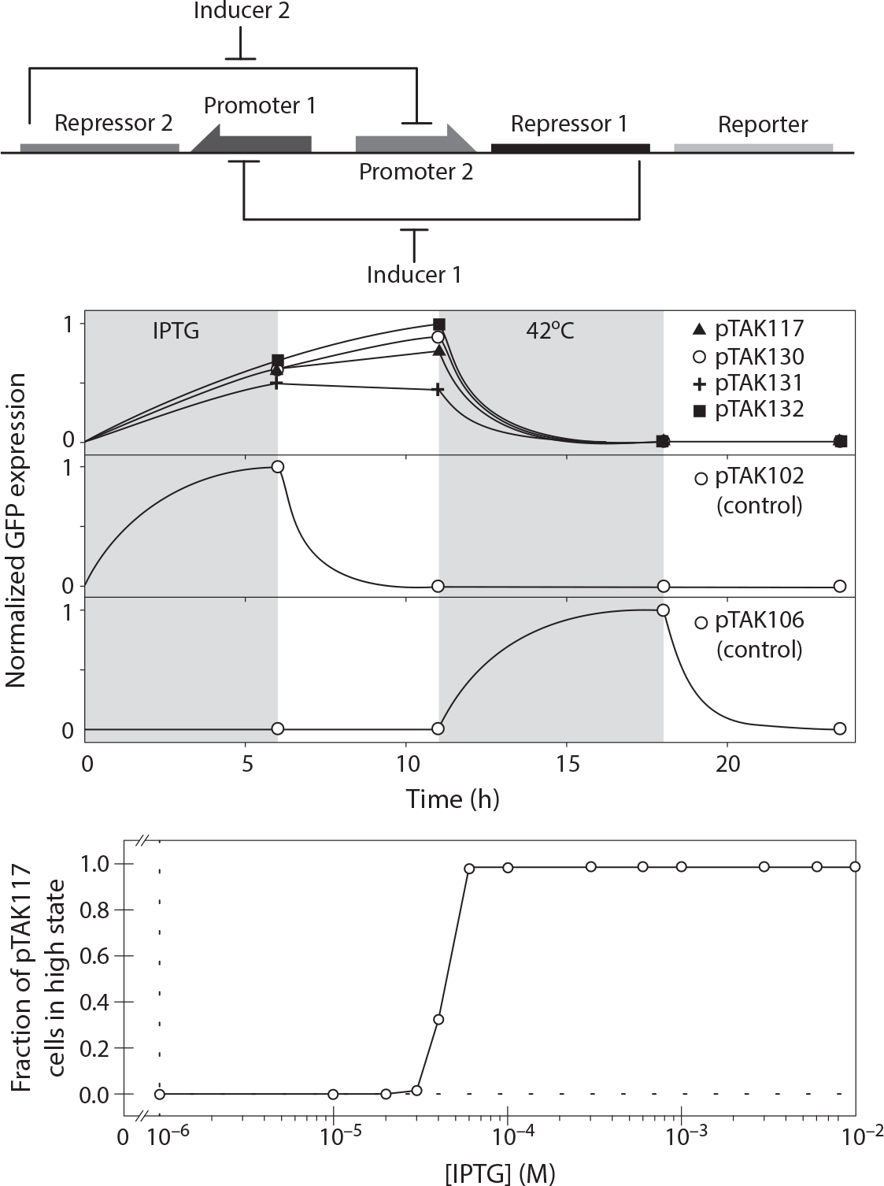
Design and performance of a synthetic gene expression switch. Incorporation of two mutual repressors leads to a stable toggle in output in response to the transient presence of input inducer. The sharp change in expression level of a reporter gene as inducer increases is an intentional feature of the system, designed with the help of a simple mathematical model of gene expression dynamics [3] .

Example 1-3Protein traffickingAll cells transport proteins to desired subcellular locations. Prokaryotes route proteins either to the extracellular space or cytoplasmic compartment, while eukaryotes possess a more intricate transportation system for movement to numerous, distinct membrane-bound organelles. Relocalization drives various biological processes, such as the receptor endocytic trafficking pathway shown in . Mathematical models of protein trafficking are valuable tools for analyzing and understanding these events and will be elaborated on in chapter 5.

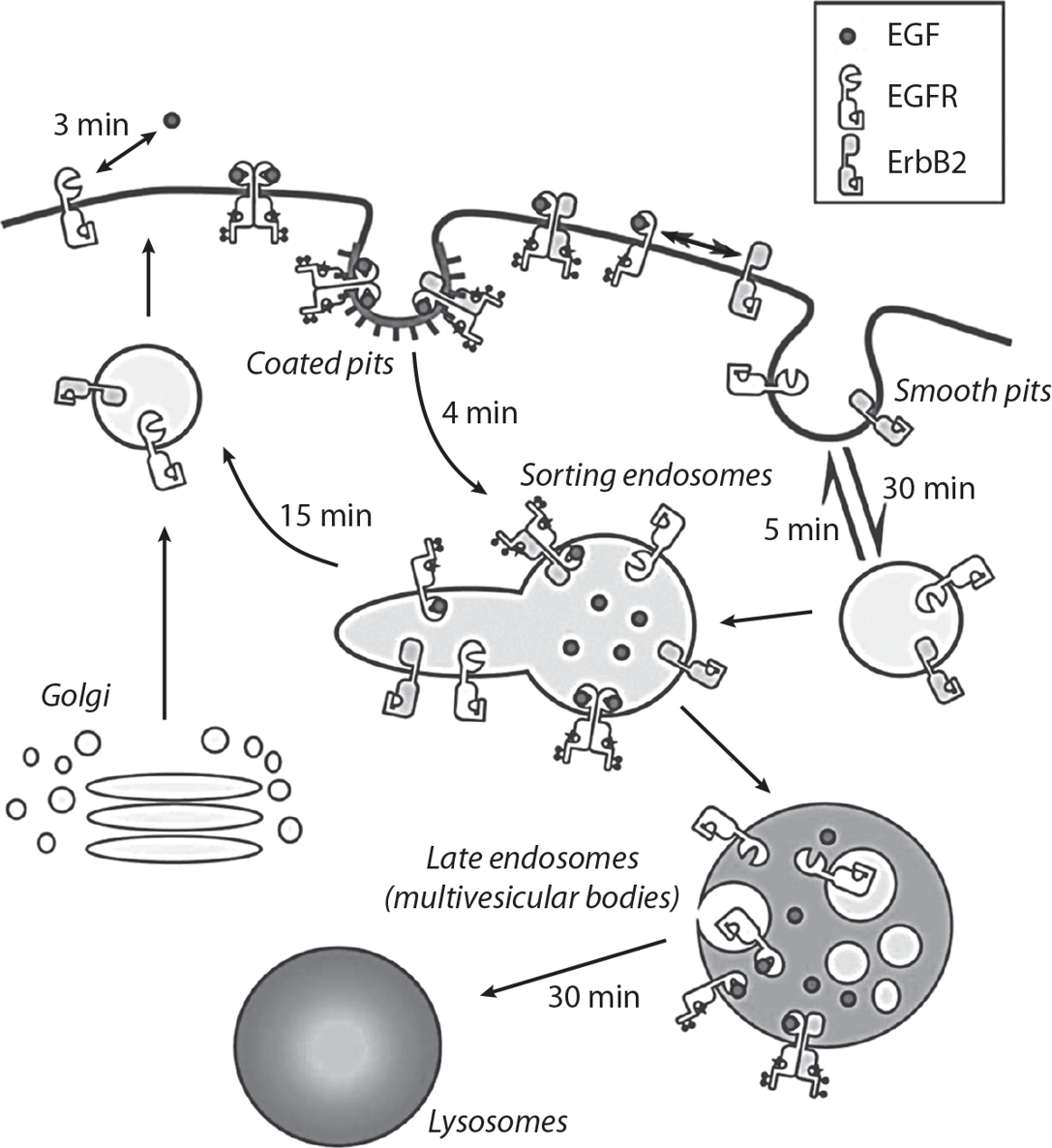
Schematic diagram of the vesicular transport pathways for cell-surface receptors [4] . Internalization and degradation following growth factor binding serves as a negative feedback function to return the system to steady state following a transient pulse of growth factor exposure. Each of the complex vesicular transport events represented by arrows in the figure, to a first approximation, can be described as a single pseudochemical reaction characterized with a single rate constant or characteristic time scale.

Example 1-4Cell signalingCells must respond to changes in their environment by altering gene expression. Transduction of information from the cell surface, where environmental inputs are generally sensed, to the cells DNA, where changes in gene expression are typically effected, is often via a chain of protein binding and covalent modification events. As described in chapter 4, such events frequently involve the enzymatic addition or removal of a phosphate group from tyrosine, serine, and threonine side chains in a series of proteins. This process is termed cell signaling, and a schematic of the typical components is shown in . The outcomes of cell signaling events can be among the most dramatic biological functions, including the life or death of the cell. Mathematical models of these events, considered in chapter 6, can be useful in understanding the relationship between time-varying inputs and the resulting effects on gene expression.