Copyright
Elsevier
Radarweg 29, PO Box 211, 1000 AE Amsterdam, Netherlands
The Boulevard, Langford Lane, Kidlington, Oxford OX5 1GB, United Kingdom
50 Hampshire Street, 5th Floor, Cambridge, MA 02139, United States
Copyright 2023 Elsevier Inc. All rights reserved.
No part of this publication may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or any information storage and retrieval system, without permission in writing from the publisher. Details on how to seek permission, further information about the Publishers permissions policies and our arrangements with organizations such as the Copyright Clearance Center and the Copyright Licensing Agency, can be found at our website: www.elsevier.com/permissions.
This book and the individual contributions contained in it are protected under copyright by the Publisher (other than as may be noted herein).
Notices
Knowledge and best practice in this field are constantly changing. As new research and experience broaden our understanding, changes in research methods, professional practices, or medical treatment may become necessary.
Practitioners and researchers must always rely on their own experience and knowledge in evaluating and using any information, methods, compounds, or experiments described herein. In using such information or methods they should be mindful of their own safety and the safety of others, including parties for whom they have a professional responsibility.
To the fullest extent of the law, neither the Publisher nor the authors, contributors, or editors, assume any liability for any injury and/or damage to persons or property as a matter of products liability, negligence or otherwise, or from any use or operation of any methods, products, instructions, or ideas contained in the material herein.
ISBN: 978-0-12-823889-9
For information on all Elsevier publications visit our website at https://www.elsevier.com/books-and-journals

Publisher: Charlotte Cockle
Acquisitions Editor: Graham Nisbet
Editorial Project Manager: Aleksandra Packowska
Production Project Manager: Kamesh Ramajogi
Cover Designer: Miles Hitchen
Typeset by STRAIVE, India
Acknowledgment
The authors thank the editorial team for their kind support and patience during the making of this work.
1: Introduction to optimization techniques for sizing and management of integrated power systems
Abstract
In this chapter, the authors briefly describe some of the most popular heuristic techniques, including ant colony optimization algorithm, genetic algorithm, gravitational search algorithm, and particle swarm optimization (PSO), among many others. In addition, the basic implementation of PSO is described and illustrated by solving several optimization problems considering the Griewank, Rastrigin, Rosenbrock, Ackley, and Schwefel test functions. In addition, the economic dispatch problem with prohibited operating zones and valve-point loading is used to illustrate PSO capabilities, observing reasonable results. Finally, the daily management of battery energy storage devices in an isolated hybrid energy system is also discussed.
Keywords
Heuristic techniques; Particle swarm optimization; Economic dispatch; Generator prohibited operating zones; Generator valve-point loading
1.1: Heuristic optimization techniques
With the progress of science and technology, investigators from different fields have created a vast family of heuristics based on natural processes. These optimization techniques have been used in the solution of many problems in electrical engineering. In this section, we briefly describe the working principles of some of the most important algorithms. Most of the mathematical formulations presented in this section are used for illustrative purposes without following any strict format.
1.1.1: Ant Colony optimization algorithm
A popular method known as the ant system () is inspired by the behavior and aptitudes of ant colonies. Ant colony optimization (ACO) is a population-based algorithm with versatility and robustness. It can be applied to many combinatory problems with only a limited number of changes in its structure.
In the ACO, each ant is considered as an agent participating in the search process. Pheromone trails inspire information exchange among the agents. The ants use these trails in the colony to share information about the shortest route to the food source. Thus, an ant on the optimal path follows a strong pheromone trail left by the rest of the colony, while an ant following a weak trail moves randomly. It is essential to highlight that an ant on a determined route also leaves its own pheromone trail on the way. The accumulative quantity of pheromones on a specific route determines how attractive this route is for the colony.
The intensity of the trail (ij) laid by the ants when they travel from a point i to j at a determined time t after n iterations of the algorithm (every n iterations the ants complete a tour) is shown in Eq. ):
ijt+n=ijt+ij
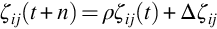 (1.1)
(1.1)
where is a parameter used to model the evaporation of the trail once the ants have completed a tour. This means between the intervals t and t + n. Furthermore, ij is the cumulative amount of pheromones laid by the group between the steps t and t + n.
Regarding the agent model, this is very basic. Each ant or agent makes its next movement according to a probability determined by the distance to the next stage of the route and the trail left by other ants that previously stopped at that stage. Even when the mathematical model is simple, the work of a massive number of agents in a collective and consolidated manner makes ACO a powerful optimization tool. A positive feedback loop mathematically represents the cumulative effect of a pheromone trail over a specific route. The probability of following this route increases with the number of ants that have chosen it.
Although natural ant colonies inspire the algorithm, it employs artificial ones. Artificial ant colonies live in an environment with discrete time, have limited memory, and are not blind. Additionally, the feasibility of each route or solution to the optimization problem is forced using a tabu list.
As previously stated, the probability of an ant transitioning from one stage to another one depends essentially on the pheromone trail and the distance. To this end, the decision maker (DM) adjusts several parameters related to the trail, the visibility of the next stage, the persistence of the trail, and the amount of pheromone left by the other ants.
Eq. ) shows the probability (pijk(t)) of moving from a point i to j at time t for the ant k. This is the expression for valid transitions, which are included using a tabu list. The parameters and are used to represent the importance of the pheromone trail and route visibility (ij).
pijkt=ijtijkiktik
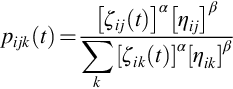











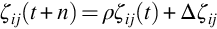 (1.1)
(1.1)