Introductory
Discrete Mathematics
V. K. Balakrishnan
DOVER PGBUCATIONS, INC.
New York
Copyright
Copyright 1991 by V. K. Balakrishnan.
All rights reserved.
Bibliographical Note
This Dover edition, first published in 1996, is an unabridged, corrected republication of the work first published by Prentice Hall, Englewood Cliffs, N.J., 1991.
Library of Congress Cataloging-in-Publication Data
Balakrishnan, V.K., date.
Introductory discrete mathematics / V. K. Balakrishnan.
p. cm.
An unabridged, corrected republication of the work first published by Prentice Hall, Englewood Cliffs, N.J., 1991T.p. verso.
Includes bibliographical references (p. - ) and index.
eISBN-13: 978-0-486-14038-4
1. Mathematics. 2. Computer scienceMathematics. I. Title.
QA39.2.B357 1996
Manufactured in the United States by Courier Corporation
69115205
www.doverpublications.com
To Geeta
Contents
Preface
Introductory Discrete Mathematics is a concise text for a discrete mathematics course at an introductory level for undergraduate students in computer science and mathematics. The essential components of any beginning level discrete mathematics curriculum are combinatorics, graph theory with applications to some standard network optimization problems, and algorithms to solve these problems. In this book the stress is on these core components. Both the Association for Computing Machinery and the Committee for the Undergraduate Program in Mathematics recognize the vital role of an undergraduate course in discrete methods that introduces the student to combinatorial mathematics and to algebraic and logical structures focusing on the interplay between computer science and mathematics.
The material in serves as an introduction to the fundamental operations involving sets and the principle of mathematical induction. For those students familiar with the topics discussed here, this is essentially a chapter for review.
The standard topics in combinatorics in any course on discrete mathematics . These topics include basic counting principles, permutations, combinations, the inclusion-exclusion principle, generating functions, recurrence relations, and an introduction to the analysis of algorithms. The role of applications is emphasized wherever possible. There are more than 200 exercises at the end of these chapters. Each counting problem requires its own special insight, and it is advantageous for the student to work out several of these problems.
In the next three chapters is a survey of graphs and digraphs. We begin with treating graphs and digraphs as models of real-world phenomena by giving several examples. The connectedness properties of graphs and digraphs are studied. Basic results and applications of graph coloring and of Eulerian and Hamiltonian graphs are presented with a stress on applications to coding and other related problems. Two important problems in network optimization are the minimal spanning tree problem and the shortest distance problem; they are covered in the last two chapters. The approach to compute the complexity of algorithms in these chapters is more or less informal.
A very brief nontechnical exposition of the theory of computational complexity and NP-completeness is outlined in the appendix.
It is possible to cover the topics presented in this book as a one-semester course by skipping some sections if necessary. Of course it is for the instructor to decide which sections she or he may skip.
My chief acknowledgment is to the students who have studied discrete mathematics with me at the University of Maine during the past decade. They taught me how to teach. Their contributions and encouragement are implicit on every page. In particular, I would like to mention the names of Rajesh and Thananchayan. My scientific indebtedness in this project encompasses many sources including the articles and books listed in the bibliography. If there are errors or misleading results, the blame of course falls entirely on my shoulders. Finally, it goes without saying that I owe a great deal to the interest and encouragement my family has shown at every stage of this work.
V. K. Balakrishnan
Set Theory and Logic
0.1 INTRODUCTION TO SET THEORY
The concept of a set plays a very significant role in all branches of modern mathematics. In recent years set theory has become an important area of investigation because of the way in which it permeates so much of contemporary mathematical thought. A genuine understanding of any branch of modern mathematics requires a knowledge of the theory of sets for it is the common foundation of the diverse areas of mathematics. Sets are used to group distinct objects together. It is necessary that the objects which belong to a set are well-defined in the sense that there should be no ambiguity in deciding whether a particular object belongs to a set or not. Thus, given an object, either it belongs to a given set or it does not belong to it. For example, the first five letters of the English alphabet constitute a set which may be represented symbolically as the set {a, b, c, d, e}. An arbitrary object belongs to this set if and only if it is one of these five letters. These five distinct objects can appear in any order in this representation. In other words, this set can also be represented by {d, b, a, e, c}. The objects that belong to a set need not possess a common property. Thus the number 4, the letter x, and the word book can constitute a set S which may be represented as S = {x, book, 4}. A particular day may be cold for one person and not cold for another, so the collection of cold days in a month is not a clearly defined set. Similarly, the collection of large numbers and the collection of tall men are also not sets.
The term object has been used here without specifying exactly what an object is. From a mathematical point of view, set is a technical term that takes its meaning from the properties we assume that sets possess. This informal description of a set, based on the intuitive notion of an object, was first given by the German mathematician Georg Cantor (18451918) toward the end of the nineteenth century and the theory of sets based on his version is known as naive set theory. In Cantors own words, a set is bringing together into a whole of definite well-defined objects of our perception and these objects are the elements of the set. The sets considered in this book can all be viewed in this framework of Cantors theory.
Thus a set is a collection of distinct objects. The objects in a set are called the elements or members of the set. If x is an element of a set A, we say that xbelongs to A, and this is expressed symbolically as x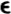 A. The notation
A. The notation 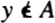 denotes that y is not an element of the set A.
denotes that y is not an element of the set A.
Finite and Infinite Sets
A set is finite if the number of elements in it is finite. Otherwise, it is an
















 A. The notation
A. The notation 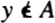 denotes that y is not an element of the set A.
denotes that y is not an element of the set A.