Sunil Tanna - Amazing Math: Introduction to Platonic Solids

Amazing Math:

Introduction to Platonic Solids

Copyright & Other Notices

Published in 2014 by Answers 2000 Limited

Copyright 2014, Sunil Tanna

Sunil Tanna has asserted his right to be identified as the author of this Work in accordance with the Copyright, Designs, and Patents Act 1988.

Information in this book is the opinion of the author, and is correct to the best of the author's knowledge, but is provided "as is" and without warranty to the maximum extent permissible under law. Content within this book is not intended as legal, tax, financial, medical, or any other form of professional advice.

While we have checked the content of this book carefully, in any educational book there is always the possibility of typographical errors, or other errors or omissions. We apologize if any such errors are found, and would appreciate if readers inform of any errors they might find, so we can update future editions/updates of this book.

Answers 2000 Limited is a private limited company registered in England under company number 3574155. Address and other information about information about Answers 2000 Limited can be found at www.ans2000.com

Updates, news & related resources from the author can be found at http://www.suniltanna.com/platonic

Information about other math books by the same author can be found at http://www.suniltanna.com/math

Introduction

For some time now, I have been tutoring both adults and children in math and science. As a result, I have discovered that many people of all ages have a latent interest (and talent) in mathematics that is somehow never got fully awoken while in school.

Because of my experience tutoring, I have been gradually been developing a series of books on mathematical and science topics (a full list of my books can be found on my website at http://www.suniltanna.com ). Most of my books are intended to teach specific topics and techniques, but I have also written others intended to awaken a student's interest in these subjects and broaden their horizons.

This book is about a fascinating mathematical topic Platonic solids which are a particular kind of 3-dimensional shapes. These shapes are not only important mathematically, but are also found in the natural world, and also have applications in science and technology. However, in my experience most people have never really considered these objects in detail, or as a unified group of related shapes.

When you review the Platonic solids, I am confident that you will recognize some of them and not just the cube for example, if you have ever played a role-playing game such as Dungeons & Dragons, the shapes of most of the polyhedral dice are all based on Platonic Solids.

In this book, among other things you will learn:

• What the Platonic solids are
• The history of the discovery of Platonic solids
• The common features of all Platonic solids
• The geometrical details of each Platonic solid
• Examples of where each type of Platonic solid occurs in nature
• How we know there are only five types of Platonic solid (geometric proof)
• A topological proof that there are only five types of Platonic solid
• What are dual polyhedra
• What is the dual polyhedron for each of the Platonic solids
• The relationships between each Platonic solid and its dual polyhedron
• How to calculate angles in Platonic solids using trigonometric formulae
• The relationship between spheres and Platonic solids
• How to calculate the surface area of a Platonic solid
• How to calculate the volume of a Platonic solid
• An introduction to some other interesting types of polyhedra prisms, antiprisms, Kepler-Poinsot polyhedra, Archimedean solids, Catalan solids, Johnson solids, and deltahedra.

Although this is a book about a mathematical topic, please do not get the impression that it is aimed only at math experts. Even if you have only ever studied (or are currently studying) high school math, then you should be able to make sense of this book. Moreover, even if your high school math is a bit rusty, I have even included a brief recap of some necessarily underlying mathematical concepts such as trigonometric operations (sine, cosine, etc.) and radians.

I hope you enjoy this book, which is one of several books that I have written.

• If you want to find out about my math books, please visit: http://www.suniltanna.com/math
• For my science books, please visit: http://www.suniltanna.com/science

Introducing Platonic Solids

Platonic solids are 3-dimensional shapes whose faces are all the same size and shape. There are 5 Platonic solids:

• Regular tetrahedron (also known as "triangular pyramid") - A shape with 4 faces, each face being a triangle
• Regular octahedron (also known as "square bipyramid") A shape with 8 faces, each face being a triangle
• Regular icosahedron A shape with 20 faces, each face being a triangle
• Regular hexahedron (also known as "cube") A shape with 6 faces, each face being a square
• Regular dodecahedron A shape with 12 faces, each face being a pentagon

In the next chapter, we will develop a more rigorous mathematical definition of Platonic solids, and see what links these particular 5 shapes and no others.

Let's get started!

Sculpture based of the five Platonic solids in the Steinfurter Bagno park, near Burgsteinfurt, Germany:

What are Platonic Solids?

In the last chapter, I listed the 5 Platonic solids, without really giving too many precise details or explaining why they are related. In this chapter, we will briefly recap some fundamental concepts in geometry, and then see how Platonic solids are defined in terms of these concepts.

You will no doubt recall that a polygon is a 2-dimensional shape (" plane figure ") made by joining straight line segments so as to form a closed loop. A regular polygon is one where all the line segments are of equal length, and all the angles between line segments where they meet at each vertex (plural: vertices ) are equal.

Examples of regular polygons include

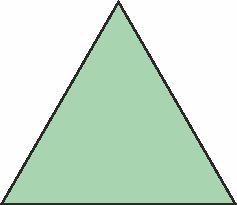
• Equilateral triangles a 3-sided shape (triangle) with 3 equal sides, and a 60 angle at every vertex

• Squares a 4-sided shape (quadrilateral) with 4 equal sides, and a 90 angle at every vertex

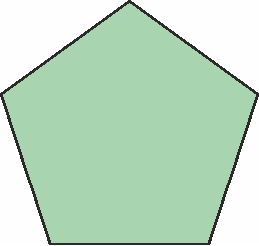
• Regular pentagons a 5-sided shape with 5 equal sides, and a 108 angle at every vertex

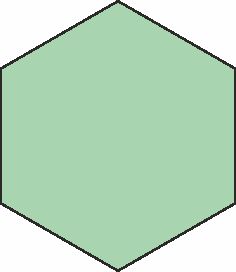
• Regular hexagons a 6-sided shape with 6 equal sides, and a 120 angle at every vertex

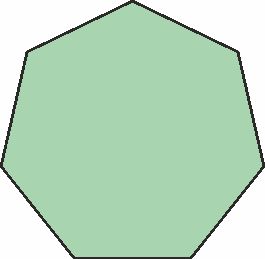
• Regular heptagons a 7-sided shape with 7 equal sides, and a 128.57 (approximately) angle at every vertex

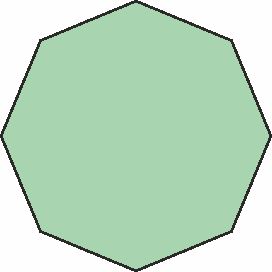
• Regular octagons an 8-sided shape with 8 equal sides, and a 135 angle at every vertex