
SHAPES OF IMAGINATION
SHAPES OF IMAGINATION
Calculating in Coleridges Magical Realm
George Stiny
The MIT Press
Cambridge, Massachusetts
London, England
2022 Massachusetts Institute of Technology
This work is subject to a Creative Commons CC-BY-NC-ND license.
Subject to such license, all rights are reserved.

The MIT Press would like to thank the anonymous peer reviewers who provided comments on drafts of this book. The generous work of academic experts is essential for establishing the authority and quality of our publications. We acknowledge with gratitude the contributions of these otherwise uncredited readers.
This book was set in ITC Stone Serif Std and ITC Stone Sans Std by New Best-set Typesetters Ltd.
Library of Congress Cataloging-in-Publication Data
Names: Stiny, George, author.
Title: Shapes of imagination : calculating in Coleridges magical realm / George Stiny.
Description: Cambridge, Massachusetts : The MIT Press, [2022] | Includes bibliographical references and index.
Identifiers: LCCN 2021046826 | ISBN 9780262544139 (paperback)
Subjects: LCSH: ShapesDesignArt. | Geometrical modelsDesignArt. | Creation (Literary, artistic, etc.)Mathematics. | AestheticsData processing.
Classification: LCC QA445 .S765 2022 | DDC 516dc23/eng/20211214
LC record available at https://lccn.loc.gov/2021046826
10987654321
d_r0
To Lionel March
in pursuit of Albertis delight in lines and numbers.
On the imagination, or esemplastic power
The IMAGINATION then I consider either as primary, or secondary. The primary IMAGINATION I hold to be the living Power and prime Agent of all human Perception, and as a repetition in the finite mind of the eternal act of creation in the infinite I A M . The secondary I consider as an echo of the former, co-existing with the conscious will, yet still as identical with the primary in the kind of its agency, and differing only in degree, and in the mode of its operation. It dissolves, diffuses, dissipates, in order to re-create; or where this process is rendered impossible, yet still at all events it struggles to idealize and to unify. It is essentially vital, even as all objects (as objects) are essentially fixed and dead.
FANCY, on the contrary, has no other counters to play with, but fixities and definites. The Fancy is indeed no other than a mode of Memory emancipated from the order of time and space; and blended with, and modified by that empirical phenomenon of the will, which we express by the word CHOICE. But equally with the ordinary memory it must receive all its materials ready made from the law of association.
Samuel Taylor Coleridge
Contents
Preface
This book consists of one longish essay, Shape Grammars: Seven Questions and their Short Answers, and three supporting exhibits that are each self-contained yet invariably drawn into one another and into my seven answersTheory, Observations, and Pedagogy. In my questions and answers, I make the case for visual calculating with rules in shape grammars, and art and design, as a single enterprise in which everything aligns coequally. In art, theres the complete sweep of visual things, and in design, a steady reminder of making and material, and function and use. The agreed approach to calculating, and art and design is to run the former through the latter, so that art and design conform fully to what calculating allows in terms of given axioms and prior invariants. The claim today is that calculating in computers includes everything we see and do, according to custom and plan. In fact, computers take away the looking to open up art and design to art experts and everyone else, and to barter and trade what the fickle eye feels, for steady truth. (This is how the Rijksmuseum explains the use of computers in its current imaging and restoration of The Night Watch. The popular title of Rembrandts painting may be mistaken in an unexpected way. As soon as computers take away the looking, theres nothing to watch nor anything to seenight or day.) The hoo-ha around this is incrediblethat the extent of known to new is within the reach of data and machine learning, that there are training sets to define it, and that nothing else is needed. Time will tell how far this vast ambition goes without slowing down. My approach in shape grammars is just the oppositeseeing informs calculating in art and design, so that calculating overtakes computers and what they hold, whether in logic or with data and learning. This is the only way I know to make calculating, and art and design coincide. There are many strands to this that bring in strange and wonderful things. These strands may seem very different, maybe irreconcilableseeing that theyre really not and how they overlap and interlace points to my key aims and goals. It will soon be apparent that I find scant to recommend in proven disciplineseven sporting different hats on different days, a physicist now and a painter tomorrow. Nor am I drawn to interdisciplinary work that only serves to reinforce separate methods and results in a combinatorial scheme, where everyone is an expert in his/her own area with no incentive to erase known boundaries, so that new configurations emerge and re-form freely in a totally seamless whole. This draws in diverse fields of interest to put them together in a single synthesis (sketch) thats inherently ambiguousfor re-division and ongoing description outside of familiar taxonomies (trees, topologies, and graphs, etc.) that rely on fixed differences to map underlying relationships. (The kind of relationship that strikes me most is conspicuous in metaphor and figuration, and runs throughout drawing and painting, and visual expression in general. More than a hundred years ago, the analytic philosopher G. E. Moore described it rather neatly, in an understandably wary account of something elseorganic unity for living/purposeful things, that eludes mechanical relations like the combinatorial ones favored in logic and indispensable for computers and taxonomies. Somehow, reuse produces a positive result, as it dodges the egregious charge of plagiarism. Moores description begs to be tried anew, to skew its original drift and purpose, and to steer past its provenance. Each relationship of the kind I have in mind is supposed to be a relation which alters the things it relates, so that it is not they, but some [number of] other things which are related. Maybe this is an example of itself that shows what it means, as Moores intentions evolve into my meaning to change the one into the other. Its funny how inconstant words can be, even the philosophers. Or maybe its Oscar Wilde, who extends meaning beyond intentions in his aesthetic formula for beautiful form, to pictures and poems, etc.to see things as in themselves they really are not. This is limitless for most things, and especially in pictures; simple shapes are enough, drawing them with merely a handful of straight linessurprises burst into view, far too numerous to overlook and too fascinating to ignore. A pair of polygonal Ls
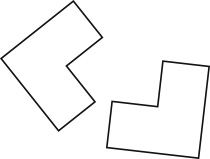
in another relation
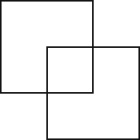
Next page










