Contents
Contents
Measuring Time
Frequency measurements and related developments in physics
Masatoshi Kajita
National Institute of Information and Communications Technology, Tokyo, Japan
IOP Publishing, Bristol, UK
IOP Publishing Ltd 2018
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior permission of the publisher, or as expressly permitted by law or under terms agreed with the appropriate rights organization. Multiple copying is permitted in accordance with the terms of licences issued by the Copyright Licensing Agency, the Copyright Clearance Centre and other reproduction rights organisations.
Permission to make use of IOP Publishing content other than as set out above may be sought at permissions@iop.org.
Masatoshi Kajita has asserted his right to be identified as the author of this work in accordance with sections 77 and 78 of the Copyright, Designs and Patents Act 1988.
ISBN 978-0-7503-2124-2 (ebook)
ISBN 978-0-7503-2122-8 (print)
ISBN 978-0-7503-2123-5 (mobi)
DOI 10.1088/978-0-7503-2124-2
Version: 20180901
IOP Expanding Physics
ISSN 2053-2563 (online)
ISSN 2054-7315 (print)
British Library Cataloguing-in-Publication Data: A catalogue record for this book is available from the British Library.
Published by IOP Publishing, wholly owned by The Institute of Physics, London
IOP Publishing, Temple Circus, Temple Way, Bristol, BS1 6HG, UK
US Office: IOP Publishing, Inc., 190 North Independence Mall West, Suite 601, Philadelphia, PA 19106, USA
Acknowledgment
The research activity of the author is supported by a Grant-in-Aid for Scientific Research (B) (Grant No. JP 17H02881), a Grant-in-Aid for Scientific Research (C) (Grant Nos. JP 17K06483 and 16K05500), and a Grant-in-Aid for Exploratory Research (Grant No. JP15K13545) from the Japan Society for the Promotion of Science (JSPS). The author is highly appreciative of discussions with Y Yano, T Ido, N Ohtsubo, Y Li, H Hachisu, S Nagano, and M Hara, all from the NICT, Japan, as well as T Aoki (University of Tokyo), M Yasuda (AIST, Japan), and A Onae (AIST, Japan; passed away 12 June 2017). The author is grateful to K Kameta and J Navas (IOP Publishing, UK) for the opportunity to write this book.
Author biography
Masatoshi Kajita
Born and raised in Nagoya, Japan, Dr Kajita graduated from the Department of Applied Physics at the University of Tokyo in 1981 and obtained his PhD from the Department of Physics at the University of Tokyo in 1986. After working at the Institute for Molecular Science, he joined the Communications Research Laboratory (CRL) in 1989. In 2004, the CRL was renamed the National Institute of Information and Communications Technology (NICT). In 2009, he was a guest professor at the University of Provence, Marseille, France.
IOP Publishing
Measuring Time
Frequency measurements and related developments in physics
Masatoshi Kajita
Chapter 1
Standards of physical quantities
1.1 Introduction
Physics concerns the laws of nature, from which we can make predictions and retrodictions of the behavior of phenomena. Researchers seek laws in the phenomena that they experience around them. Experimentalists confirm the laws and look for new phenomena whereas theoreticians seek unknown phenomena based on the laws or by extending them. With the discovery of new phenomena that cannot be described by established laws, new models are developed to explain them and thus we take new steps in advancing physics knowledge.
Measurements of physical quantities are important in describing phenomena in detail. For example, the empirical law the distance traveled by a falling body is directly proportional to the square of the time taken in the fall was established first by Galilei through measurements of fall times and distance traveled. However, any measurement (for example, X) comes with an inherent uncertainty (X), and the measurement result should be given as XX. We must compare this measurement result with estimates given by the different models. If one model gives the value X + 1X and another model gives X + 2X, we cannot say which model is right when 1,2X < X. The model that is easiest to imagine for most scholars has been, on the whole, the one most accepted. Only after the uncertainty in the measurement has been reduced and X < 1X 2X holds, can we conclude which models to eliminate.
To discuss the uncertainty in a measurement, we must determine the standards associated with each physical quantity. Note that physics is based on three fundamental physical quantities: mass (M), length (L), and time (T). All other physical quantities are combinations of these three fundamental quantities and are given in the form Mn(M)Ln(L)Tn(T), where n(M, L, T) are the dimensions of each fundamental quantity. Several typical examples are given below:
| Velocity | M0L1T1 | Acceleration | M0L1T2 |
| Force | M1L1T2 | Energy | M1L2T2. |
Therefore, the measurement accuracy is given by the measurement accuracies to which the three fundamental physical quantities are known. The current convention is to present values of these three physical quantities using the MKS-system of units:
| Mass | kilogram | (kg) |
| Length | meter | (m) |
| Time | second | (s). |
There are questions as to how accurately these three fundamental quantities are determined. We need to consider the standard for each physical quantity so that the measurement of time/length/mass by any clock/ruler/solid metering device should be equal. With one clock, we read the time trusting this clock is correct. However, with two clocks displaying different times (figure ), at least one clock has problems with accuracy due to mechanical problems or the initial settings. We do not know which clock, if either, is correct, but from their time differences, we can imagine the clocks have an associated uncertainty.
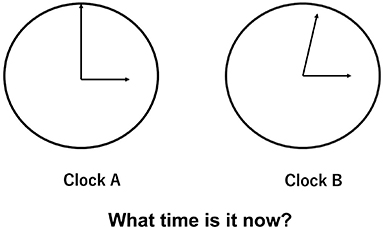
Figure 1.1. A situation where two clocks display different times. The question is which clock, if either, tells the actual time.
Next, we introduce standards by which the units of the three fundamental quantities are defined.
1.2 The time and frequency standard
The standard for time and frequency has changed over the centuries (figure ].