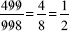Lehmann Ingmar - Mathematical curiosities: a treasure trove of unexpected entertainments
Here you can read online Lehmann Ingmar - Mathematical curiosities: a treasure trove of unexpected entertainments full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Amherst, New York, year: 2014, publisher: Prometheus Books, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Mathematical curiosities: a treasure trove of unexpected entertainments
- Author:
- Publisher:Prometheus Books
- Genre:
- Year:2014
- City:Amherst, New York
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Mathematical curiosities: a treasure trove of unexpected entertainments: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Mathematical curiosities: a treasure trove of unexpected entertainments" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
An innovative and appealing way for the layperson to develop math skills--while actually enjoying it
Most people agree that math is important, but few would say its fun. This book will show you that the subject you learned to hate in high school can be as entertaining as a witty remark, as engrossing as the mystery novel you cant put down--in short, fun! As veteran math educators Posamentier and Lehmann demonstrate, when you realize that doing math can be enjoyable, you open a door into a world of unexpected insights while learning an important skill.
The authors illustrate the point with many easily understandable examples. One of these is what mathematicians call the Ruth-Aaron pair (714 and 715), named after the respective career home runs of Babe Ruth and Hank Aaron. These two consecutive integers contain a host of interesting features, one of which is that their prime factors when added together have the same sum.
The authors also explore...
Lehmann Ingmar: author's other books
Who wrote Mathematical curiosities: a treasure trove of unexpected entertainments? Find out the surname, the name of the author of the book and a list of all author's works by series.












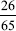 , and did it in the following way:
, and did it in the following way: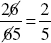
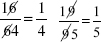
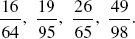
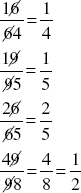
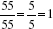 as an illustration of this type of cancellation. This will, clearly, hold true for all two-digit multiples of eleven.
as an illustration of this type of cancellation. This will, clearly, hold true for all two-digit multiples of eleven.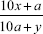 , in which the second digit of the numerator and the first digit of the denominator match.
, in which the second digit of the numerator and the first digit of the denominator match.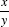 .
.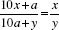 .
.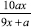 .
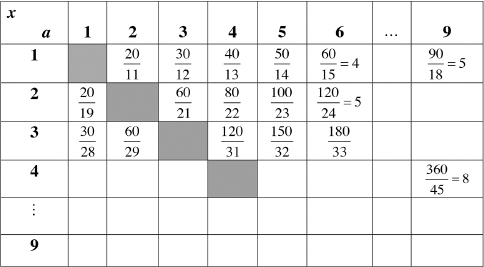
.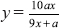 . Remember that x, y, and a must be single-digit integers. Below is a portion of the table you will be constructing. Notice that the cases where x = a are excluded, since
. Remember that x, y, and a must be single-digit integers. Below is a portion of the table you will be constructing. Notice that the cases where x = a are excluded, since 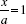 .
.
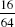 and
and 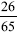 , respectively. The remaining two integral values of y will be obtained when x = 1 and a = 9, yielding y = 5, and when x = 4 and a = 9, yielding y = 8. These yield the fractions
, respectively. The remaining two integral values of y will be obtained when x = 1 and a = 9, yielding y = 5, and when x = 4 and a = 9, yielding y = 8. These yield the fractions 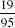 and
and 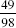 , respectively. This should convince you that there are only four such fractions composed of two-digit numbers, excluding two-digit multiples of 11.
, respectively. This should convince you that there are only four such fractions composed of two-digit numbers, excluding two-digit multiples of 11.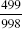 . You should find that
. You should find that