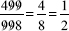The authors wish to extend sincere thanks for proofreading and extremely useful suggestions offered by Dr. Elaine Paris, emeritus professor of mathematics at Mercy College, New York. Her insight and sensitivity for the general readership has been extremely helpful. We also thank Catherine Roberts-Abel for very capably managing the production of this book, and Jade Zora Scibilia for the truly outstanding editing throughout the various phases of production. Steven L. Mitchell deserves praise for enabling us to continue to approach the general readership with yet another book demonstrating mathematical gems.
The curiosities found in arithmetic and in numbers, in general, are probably boundless. They range from peculiarities of certain numbers to number relationships stemming from ordinary arithmetic processes. What makes these so entertaining are the unexpected results that are sometimes inexplicable. In this chapter we will be presenting to you some of these many arithmetic and numeric oddities in mathematics. Some are clearly errors that lead to correct results, while others are correct workings of mathematics that lead to wildly unexpected results. In either case, we hope that through the mathematics alone you will be entertained without having to apply it to other fields in either the sciences or the real world. Our intent here is to demonstrate a special beauty that can make mathematics fascinating and enjoyable.
HOWLERS
In the early years of schooling we learned to reduce fractions to make them more manageable. For this there were specific ways to do it correctly. Some wise guy seems to have come up with a shorter way to reduce some fractions. Is he right?
He was asked to reduce the fraction 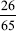 , and did it in the following way:
, and did it in the following way:
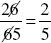
That is, he just canceled out the 6's to get the right answer. Is this procedure correct? Can it be extended to other fractions? If this is so, then we were surely treated unfairly by our elementary-school teachers, who made us do much more work. Let's look at what was done here and see if it can be generalized.
In his book Fallacies in Mathematics, E. A. Maxwell refers to these cancellations as howlers:
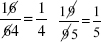
Perhaps when someone did the fraction reductions this way, and still got the right answer, it could just make you howl. This simple procedure continues to give us the correct answers: As we look at this awkwardyet easyprocedure, we could begin by reducing the following fractions to lowest terms:
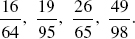
After you have reduced to lowest terms each of the fractions in the usual manner, one may ask why it couldn't have been done in the following way.

At this point you may be somewhat amazed. Your first reaction is probably to ask if this can be done to any fraction composed of two-digit numbers of this sort. Can you find another fraction (comprised of two-digit numbers) where this type of cancellation will work? You might cite  as an illustration of this type of cancellation. This will, clearly, hold true for all two-digit multiples of eleven.
as an illustration of this type of cancellation. This will, clearly, hold true for all two-digit multiples of eleven.
For those readers with a good working knowledge of elementary algebra, we can explain this awkward occurrence. That is, why are the four fractions above the only ones (comprised of different two-digit numbers) where this type of cancellation will hold true?
Consider the fraction 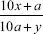 , in which the second digit of the numerator and the first digit of the denominator match.
, in which the second digit of the numerator and the first digit of the denominator match.
The above four cancellations were such that when canceling the a's the fraction was equal to 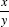 .
.
Let us explore this relationship: 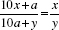 .
.
This yields y(10x+a) = x(10a+y),
10xy + ay = 10ax + xy,
9xy + ay = 10axy (9x + a) = 10ax,
and so 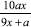 .
.
At this point we shall inspect this equation. It is necessary that x, y, and a are integers since they were digits in the numerator and denominator of a fraction. It is now our task to find the values of a and x for which y will also be integral. To avoid a lot of algebraic manipulation, you will want to set up a chart that will generate values of y from 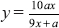 . Remember that x, y, and a must be single-digit integers. Below is a portion of the table you will be constructing. Notice that the cases where x = a are excluded, since
. Remember that x, y, and a must be single-digit integers. Below is a portion of the table you will be constructing. Notice that the cases where x = a are excluded, since 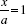 .
.
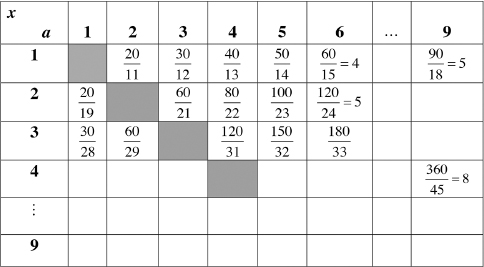
Figure 1.1
This small portion of the chart () already generated two of the four integral values of y; that is, when x = 1, a = 6, then y = 4, and when x = 2, a = 6, and y = 5. These values yield the fractions 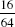 and
and 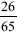 , respectively. The remaining two integral values of y will be obtained when x = 1 and a = 9, yielding y = 5, and when x = 4 and a = 9, yielding y = 8. These yield the fractions
, respectively. The remaining two integral values of y will be obtained when x = 1 and a = 9, yielding y = 5, and when x = 4 and a = 9, yielding y = 8. These yield the fractions 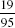 and
and 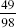 , respectively. This should convince you that there are only four such fractions composed of two-digit numbers, excluding two-digit multiples of 11.
, respectively. This should convince you that there are only four such fractions composed of two-digit numbers, excluding two-digit multiples of 11.
Let's extend this idea and investigate whether there are fractions composed of numerators and denominators of more than two digits where this strange type of cancellation holds true. Try this type of cancellation with 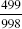 . You should find that
. You should find that 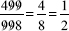


















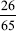 , and did it in the following way:
, and did it in the following way: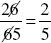
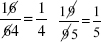
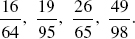

 as an illustration of this type of cancellation. This will, clearly, hold true for all two-digit multiples of eleven.
as an illustration of this type of cancellation. This will, clearly, hold true for all two-digit multiples of eleven.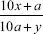 , in which the second digit of the numerator and the first digit of the denominator match.
, in which the second digit of the numerator and the first digit of the denominator match.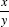 .
.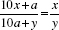 .
.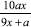 .
.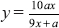 . Remember that x, y, and a must be single-digit integers. Below is a portion of the table you will be constructing. Notice that the cases where x = a are excluded, since
. Remember that x, y, and a must be single-digit integers. Below is a portion of the table you will be constructing. Notice that the cases where x = a are excluded, since 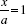 .
.
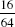 and
and 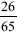 , respectively. The remaining two integral values of y will be obtained when x = 1 and a = 9, yielding y = 5, and when x = 4 and a = 9, yielding y = 8. These yield the fractions
, respectively. The remaining two integral values of y will be obtained when x = 1 and a = 9, yielding y = 5, and when x = 4 and a = 9, yielding y = 8. These yield the fractions 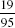 and
and 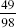 , respectively. This should convince you that there are only four such fractions composed of two-digit numbers, excluding two-digit multiples of 11.
, respectively. This should convince you that there are only four such fractions composed of two-digit numbers, excluding two-digit multiples of 11.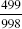 . You should find that
. You should find that