Metin Bektas - Great Formulas Explained - Physics, Mathematics, Economics

• Intensity:

Under ideal circumstances, sound or light waves emitted from a point source propagate in a spherical fashion from the source. As the distance to the source grows, the energy of the waves is spread over a larger area and thus the perceived intensity decreases. We'll take a look at the formula that allows us to compute the intensity at any distance from a source.

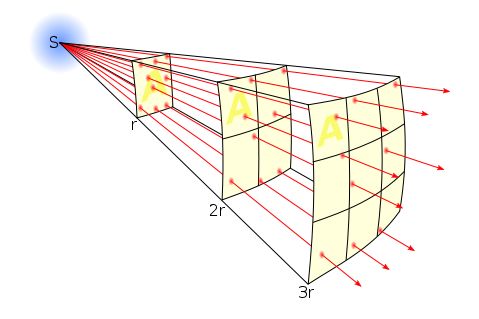
First of all, what do we mean by intensity? The intensity I tells us how much energy we receive from the source per second and per square meter. Accordingly, it is measured in the unit J per s and m2 or simply W/m2. To calculate this quantity, we need to know the power of the source P (in W) and the distance r (in m) to it.

I = P / ( 4 r )

This is one of these formulas that can quickly get you hooked on physics. It's very simple and extremely useful. In a later section you will meet the denominator again. It is the expression for the surface area of a sphere with radius r. Before we go to the examples, let's take a look at a special intensity scale that is often used in acoustics. Instead of expressing the sound intensity in the common physical unit W/m 2 , we can convert it to its corresponding decibel value dB using the following formula:

dB 120 + 4.34 ln(I)

with ln being the natural logarithm. For example, a sound intensity of I = 0.00001 W/m2 (busy traffic) translates into 70 dB. This conversion is done to avoid dealing with very small or large numbers. Here are some typical values to keep in mind:

0 dB Threshold of Hearing

20 dB Whispering

60 dB Normal Conversation

80 dB Vacuum Cleaner

110 dB Front Row at Rock Concert

130 dB Threshold of Pain

160 dB Bursting Eardrums

Now onto the examples.

----------------------

We just bought a P = 300 W speaker and want to try it out at maximal power. To get the full dose, we sit at a distance of only r = 1 m. Is that a bad idea? To find out, let's calculate the intensity at this distance and the matching decibel value.

I = 300 W / ( 4 (1 m) ) 23.9 W/m2

dB 120 + 4.34 ln(23.9) 134 dB

This is already past the threshold of pain, so yes, it is a bad idea. But on the bright side, there's no danger of the eardrums bursting. So it shouldn't be dangerous to your health as long as you're not exposed to this intensity for a longer period of time.

A side note: the speaker is of course no point source, so all these values are just estimates based on the idea that as long as you're not too close to a source, it can be regarded as a point source in good approximation. The more the source resembles a point source and the farther you're from it, the better the estimates computed using the formula will be.

----------------------

Let's reverse the situation from the previous example. Again we assume a distance of r = 1 m from the speaker. At what power P would our eardrums burst? Have a guess before reading on.

As we can see from the table, this happens at 160 dB. To be able to use the intensity formula, we need to know the corresponding intensity in the common physical quantity W/m2. We can find that out using this equation:

160 120 + 4.34 ln(I)

We'll subtract 120 from both sides and divide by 4.34:

40 4.34 ln(I)

9.22 ln(I)

The inverse of the natural logarithm ln is Euler's number e. In other words: e to the power of ln(I) is just I. So in order to get rid of the natural logarithm in this equation, we'll just use Euler's number as the basis on both sides:

e9.22 eln(I)

10,100 I

Thus, 160 dB correspond to I = 10,100 W/m2. At this intensity eardrums will burst. Now we can answer the question of which amount of power P will do that, given that we are only r = 1 m from the sound source. We insert the values into the intensity formula and solve for P:

10,100 = P / ( 4 1 )

10,100 = 0.08 P

P 126,000 W

So don't worry about ever bursting your eardrums with a speaker or a set of speakers. Not even the powerful sound systems at rock concerts could accomplish this.

----------------------

The intensity of the sunlight reaching earth is about I = 1400 W/m2. Given that the distance between earth and sun is about r = 150,000,000,000 m, what is the sun's power output? To calculate this, we again have to solve the formula for P:

I = P / ( 4 r )

P = I 4 r

With this done, getting the result is simply a matter of plugging in the given data. This leads to:

P = 1400 W/m 4 ( 150,000,000,000 m)

P 4 10 W

This value is almost beyond comprehension. In one second the sun gives off enough energy to satisfy the our current energy needs for the next 500,000 years. Unfortunately only very little of this energy actually reaches earth and only very little of that can be converted into useful energy.

----------------------

In the next section we'll look at another radially propagating wave. But hopefully you noticed that physics and math does not need to be difficult. Some of the greatest calculations can be done with a handy formula and a few lines of writing.

• Explosions:

When a strong explosion takes place, a shock wave forms that propagates in a spherical manner away from the source of the explosion. The shock front separates the air mass that is heated and compressed due to the explosion from the undisturbed air. In the picture below you can see the shock sphere that resulted from the explosion of Trinity, the first atomic bomb ever detonated.

Using the concept of similarity solutions, the physicists Taylor and Sedov derived a simple formula that describes how the radius r (in m) of such a shock sphere grows with time t (in s). To apply it, we need to know two additional quantities: the energy of the explosion E (in J) and the density of the surrounding air D (in kg/m3). Here's the formula:

r = 0.93 (E / D)0.2 t0.4

Let's apply this formula for the Trinity blast.

----------------------

In the explosion of the Trinity the amount of energy that was released was about 20 kilotons of TNT or:

E = 84 TJ = 84,000,000,000,000 J

Just to put that into perspective: in 2007 all of the households in Canada combined used about 1.4 TJ in energy. If you were able to convert the energy released in the Trinity explosion one-to-one into useable energy, you could power Canada for 60 years.

But back to the formula. The density of air at sea-level and lower heights is about D = 1.25 kg/m3. So the radius of the sphere approximately followed this law:

r = 542 t 0.4

After one second (t = 1), the shock front traveled 542 m. So the initial velocity was 542 m/s 1950 km/h 1210 mph. After ten seconds (t = 10), the shock front already covered a distance of about 1360 m 0.85 miles.

How long did it take the shock front to reach people two miles from the detonation? Two miles are approximately 3200 m. So we can set up this equation:

3200 = 542 t 0.4

We divide by 542:

5.90 t 0.4

Then take both sides to the power of 2.5:

t 85 s 1 and 1/2 minutes

----------------------

Let's look at how the different parameters in the formula impact the radius of the shock sphere:

• If you increase the time sixfold, the radius of the sphere doubles. So if it reached 0.85 miles after ten seconds, it will have reached 1.7 miles after 60 seconds. Note that this means that the speed of the shock front continuously decreases.