1. Exponents
1.1. Motivation
Identities involving exponents are part of the foundation of mathematics. Accordingly, the reader should study them carefully and in great detail. Most of what will follow, in this book and in math courses in school, requires knowledge of these identities.
1.2.
Before we get to the identities, let's have a look at the "fine print". These are conventions that you will need in order to understand and apply exponentiation rules. Let's start with the obvious. Whenever we write x, we refer to x to the power of one:
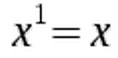
For example: 21 = 2, which you can easily check using a calculator. Since you always need to know the exponents when applying the identities, this piece of information will be helpful later on. Just as important, but less obvious, is the following piece of information.
Every number (except zero) to the power of zero is equal to one: 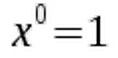 Again, you can easily check this with a calculator. Since we now know what x0 and x1 mean, let's turn to other exponents. You get x2 when you multiply a number x by itself:
Again, you can easily check this with a calculator. Since we now know what x0 and x1 mean, let's turn to other exponents. You get x2 when you multiply a number x by itself: 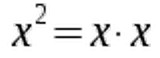 In a similar fashion you arrive at x3 when multiplying a number x by itself three times.
In a similar fashion you arrive at x3 when multiplying a number x by itself three times. 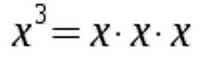 We can generalize this approach. To calculate x to the power of n, we multiply a number x by itself n-times.
We can generalize this approach. To calculate x to the power of n, we multiply a number x by itself n-times. 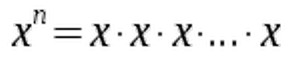 Such an expression can easily grow to a large number.
Such an expression can easily grow to a large number.
The harmless looking expression 68 already exceeds one million: 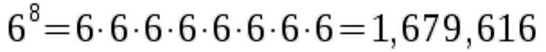 Besides x0 and x1 we can now calculate all other natural number exponents. Can an exponent be a negative number? Can it even be a fraction? Both is possible. But the above approach doesn't work here any more, since you obviously can't multiply a number by itself minus three times or one-half times. For negative exponents we use this important convention:
Besides x0 and x1 we can now calculate all other natural number exponents. Can an exponent be a negative number? Can it even be a fraction? Both is possible. But the above approach doesn't work here any more, since you obviously can't multiply a number by itself minus three times or one-half times. For negative exponents we use this important convention: 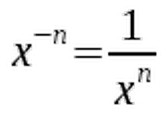 It allows us to transform negative to positive exponents. So x-n is just the reciprocal of xn. For example:
It allows us to transform negative to positive exponents. So x-n is just the reciprocal of xn. For example: 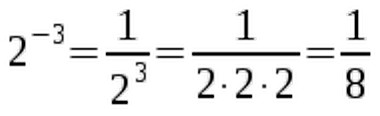 Keep this convention in mind.
Keep this convention in mind.
It will come in handy when solving problems later on. What about fractional exponents? At this point we'll limit ourselves to one special case, that is, the fraction 1/2. It just refers to the well-known square root: 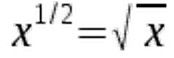 Feel free to check this using a calculator. If you type in the number 25 to the power of 1/2, the result will be 5, which is the square root of 25.
Feel free to check this using a calculator. If you type in the number 25 to the power of 1/2, the result will be 5, which is the square root of 25. 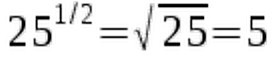 With this we conclude the section on the "fine print" and move on to the identities.
With this we conclude the section on the "fine print" and move on to the identities.
1.3.
Exponential Identities
1.3.1. First and Second Law
Quite often, for example when getting rid of brackets, we need to multiply expressions involving exponents. The
first law of exponentiation allows us to do just that:
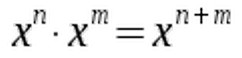
So we keep the base x and add the exponents - simple as that. A quick example:
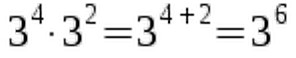
We can easily see why this works. 34 means that we multiply the number 3 by itself four times. We multiply this by 32, which is just the number 3 multiplied by itself once.
So in total we now have the number 3 six times in a row, which in short is just 36. 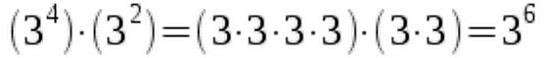 The identity also works for negative exponents:
The identity also works for negative exponents: 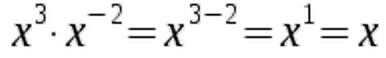 Sometimes we need to rewrite a fraction using negative exponents to apply the identity. Here's an example of this:
Sometimes we need to rewrite a fraction using negative exponents to apply the identity. Here's an example of this: 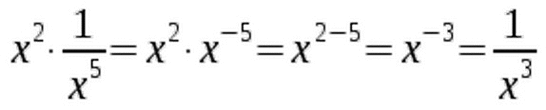 Does the identity also work for fractional exponents? It sure does.
Does the identity also work for fractional exponents? It sure does. 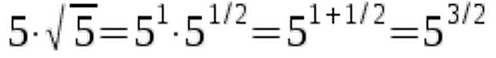 Note that it makes no difference whether the base is a variable (x, y, ...) or a specific number (3, 5, ...). Working with a variable might be more abstract, but the principle stays the same. So don't worry too much about using variables.
Note that it makes no difference whether the base is a variable (x, y, ...) or a specific number (3, 5, ...). Working with a variable might be more abstract, but the principle stays the same. So don't worry too much about using variables.
Keep in mind though that to be able to apply the first law, the expressions need to have the same base. For example, the first law can't help us when dealing with expressions such as: 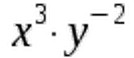 or
or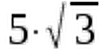 Let's move on to the second law of exponentiation. Sometimes we have to divide rather than multiply expressions that include exponents. Then we can use this rule:
Let's move on to the second law of exponentiation. Sometimes we have to divide rather than multiply expressions that include exponents. Then we can use this rule: 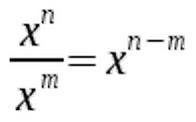 Again we keep the base x, but this time we subtract the exponents.
Again we keep the base x, but this time we subtract the exponents. 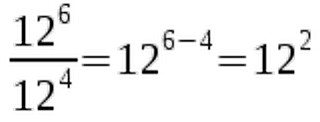 Pay close attention to the signs when using the second law.
Pay close attention to the signs when using the second law. 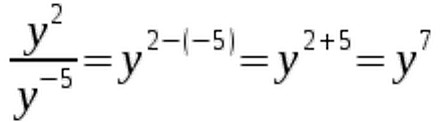 The following example demonstrates that, just like the first law, the second law also works for fractional exponents.
The following example demonstrates that, just like the first law, the second law also works for fractional exponents. 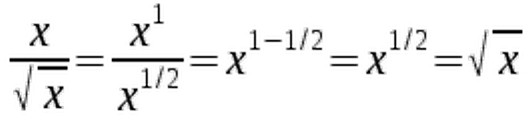 To be able to use the second law, it is vital to have expressions with the same base.
To be able to use the second law, it is vital to have expressions with the same base. 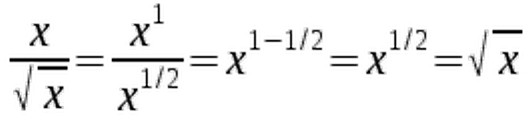 To be able to use the second law, it is vital to have expressions with the same base.
To be able to use the second law, it is vital to have expressions with the same base.
Hence, we can't use it to simplify these two expressions: 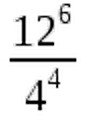










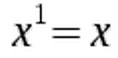 For example: 21 = 2, which you can easily check using a calculator. Since you always need to know the exponents when applying the identities, this piece of information will be helpful later on. Just as important, but less obvious, is the following piece of information.
For example: 21 = 2, which you can easily check using a calculator. Since you always need to know the exponents when applying the identities, this piece of information will be helpful later on. Just as important, but less obvious, is the following piece of information. 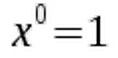 Again, you can easily check this with a calculator. Since we now know what x0 and x1 mean, let's turn to other exponents. You get x2 when you multiply a number x by itself:
Again, you can easily check this with a calculator. Since we now know what x0 and x1 mean, let's turn to other exponents. You get x2 when you multiply a number x by itself: 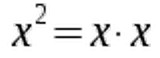 In a similar fashion you arrive at x3 when multiplying a number x by itself three times.
In a similar fashion you arrive at x3 when multiplying a number x by itself three times. 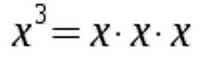 We can generalize this approach. To calculate x to the power of n, we multiply a number x by itself n-times.
We can generalize this approach. To calculate x to the power of n, we multiply a number x by itself n-times. 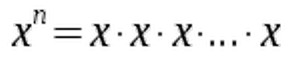 Such an expression can easily grow to a large number.
Such an expression can easily grow to a large number.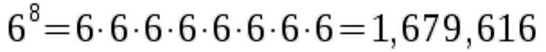 Besides x0 and x1 we can now calculate all other natural number exponents. Can an exponent be a negative number? Can it even be a fraction? Both is possible. But the above approach doesn't work here any more, since you obviously can't multiply a number by itself minus three times or one-half times. For negative exponents we use this important convention:
Besides x0 and x1 we can now calculate all other natural number exponents. Can an exponent be a negative number? Can it even be a fraction? Both is possible. But the above approach doesn't work here any more, since you obviously can't multiply a number by itself minus three times or one-half times. For negative exponents we use this important convention: 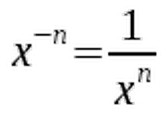 It allows us to transform negative to positive exponents. So x-n is just the reciprocal of xn. For example:
It allows us to transform negative to positive exponents. So x-n is just the reciprocal of xn. For example: 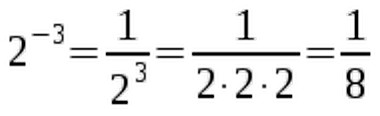 Keep this convention in mind.
Keep this convention in mind.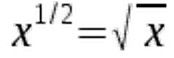 Feel free to check this using a calculator. If you type in the number 25 to the power of 1/2, the result will be 5, which is the square root of 25.
Feel free to check this using a calculator. If you type in the number 25 to the power of 1/2, the result will be 5, which is the square root of 25. 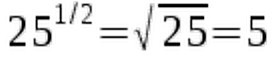 With this we conclude the section on the "fine print" and move on to the identities.
With this we conclude the section on the "fine print" and move on to the identities.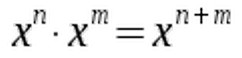 So we keep the base x and add the exponents - simple as that. A quick example:
So we keep the base x and add the exponents - simple as that. A quick example: 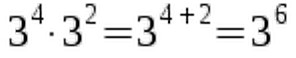 We can easily see why this works. 34 means that we multiply the number 3 by itself four times. We multiply this by 32, which is just the number 3 multiplied by itself once.
We can easily see why this works. 34 means that we multiply the number 3 by itself four times. We multiply this by 32, which is just the number 3 multiplied by itself once. 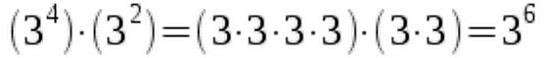 The identity also works for negative exponents:
The identity also works for negative exponents: 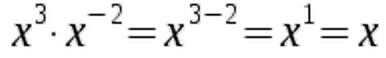 Sometimes we need to rewrite a fraction using negative exponents to apply the identity. Here's an example of this:
Sometimes we need to rewrite a fraction using negative exponents to apply the identity. Here's an example of this: 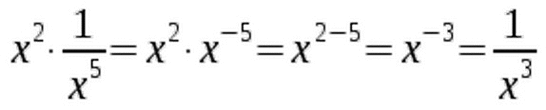 Does the identity also work for fractional exponents? It sure does.
Does the identity also work for fractional exponents? It sure does. 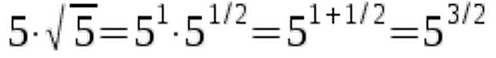 Note that it makes no difference whether the base is a variable (x, y, ...) or a specific number (3, 5, ...). Working with a variable might be more abstract, but the principle stays the same. So don't worry too much about using variables.
Note that it makes no difference whether the base is a variable (x, y, ...) or a specific number (3, 5, ...). Working with a variable might be more abstract, but the principle stays the same. So don't worry too much about using variables.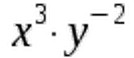 or
or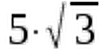 Let's move on to the second law of exponentiation. Sometimes we have to divide rather than multiply expressions that include exponents. Then we can use this rule:
Let's move on to the second law of exponentiation. Sometimes we have to divide rather than multiply expressions that include exponents. Then we can use this rule: 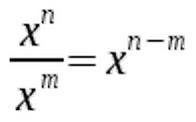 Again we keep the base x, but this time we subtract the exponents.
Again we keep the base x, but this time we subtract the exponents. 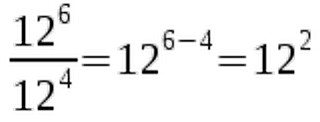 Pay close attention to the signs when using the second law.
Pay close attention to the signs when using the second law. 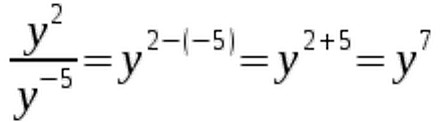 The following example demonstrates that, just like the first law, the second law also works for fractional exponents.
The following example demonstrates that, just like the first law, the second law also works for fractional exponents. 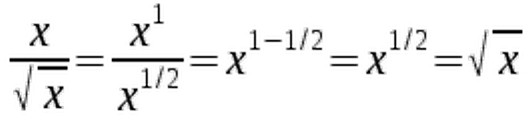 To be able to use the second law, it is vital to have expressions with the same base.
To be able to use the second law, it is vital to have expressions with the same base.