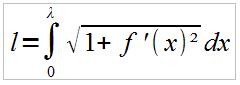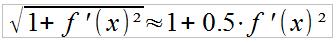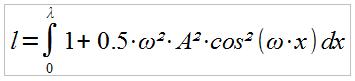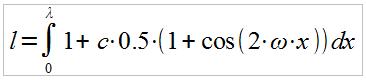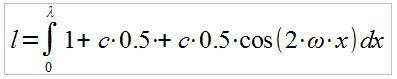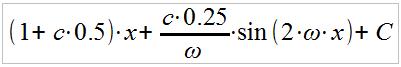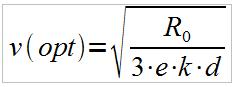Metin Bektas - Mathematical Shenanigans

Mathematical Shenanigans

• Rough Seas

Suppose you work at a company that ships goods across the ocean. Your boss asks you to cook up some equations regarding trip duration and energy requirements to go along with that. Shouldn't be too hard, right? Let's start with duration. According to map data, the distance between the to two ports of interest is d. Since the ship is able to go the constant speed v, the duration of one trip will obviously be:

t = d / v

For the energy we consult Newton. He stated that the force necessary to overcome fluid friction grows proportionally to the square of the speed: F = k v. The constant k is given by onehalf times the product of water density, the ship's drag coefficient and frontal area of the submerged part. We assume that all of these are known. Since the energy required is the product of force times distance, our ship will consume this amount during the trip:

E = k v d

This would be good enough for your boss, but you want to know what effect the presence of waves will have on these quantities. When there are waves in between the port, your ship will obviously have to travel a greater distance. Additionally to the horizontal distance, it will need to go up and down.

Water waves are in general trochoidal in shape. But, lucky for us, for smaller amplitudes they are almost sinusoidal. For the sake of computation, we have to limit ourselves to waves that are small in amplitude A compared to their wavelength . The form of the waves can be expressed by:

f(x) = A sin( x)

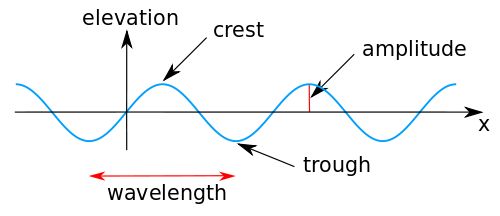
(Parameters and parts of a wave)

with the constant being given by = 2 / . What distance do we need to travel to go over one wave cycle (that is, from trough to trough)? A formula from integral calculus can help us answer that:

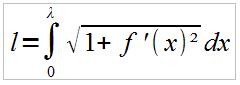
Since we are dealing with relatively small amplitudes here, we will use a Taylor approximation instead of the (analytically challenging) square root:

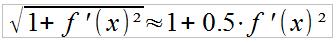
And since the derivative of f(x) is:

f '(x) = A cos( x)

We thus need to solve this integral:

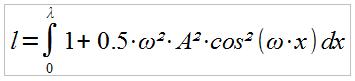
The smart way of doing this is to use the following neat trigonometric identity before tackling the integral:

cos( x) = 0.5 ( 1 + cos(2 x) )

And set:

c = 0.5 A

So we have:

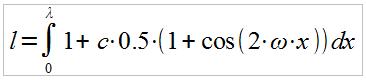
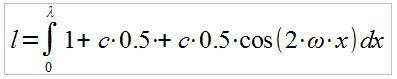
The antiderivative of the integrand is:

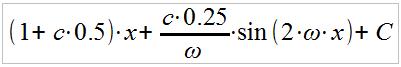
With this done, we can now easily evaluate the integral. Noticing that sin(0) = 0 and sin(2 ) = sin(4 ) = 0, this leaves us with:

l = (1 + c 0.5) = (1 + 0.25 A)

This is the distance that is covered by traveling over one sine wave with amplitude A and wave length . What does this mean for the overall distance our ship needs to travel between the two ports? We can fit the following number of waves into the horizontal distance d:

n = d /

So the overall distance the ship needs to travel in rough seas will be:

d' = n l = d / (1 + 0.25 A)

d' = d (1 + 0.25 A)

Inserting = 2 / we finally get:

d' = d (1 + A / )

So the presence of the waves increases the distance to be covered by a factor that is solely determined by the steepness (ratio of amplitude to wave length) of the waves. Is this increase in distance noticeable? Let's try it out. Suppose the waves have an amplitude of A = 0.5 m (so they are 1 m high) and wave length of = 4 m. Inserting these values, we get:

d' d 1.15

So there's a 15 % increase definitely noticeable. If the distance is 5000 km, we need to travel an extra 750 km in the above sea conditions. Since our ship will still go at its usual constant speed v, the values for the duration of the trip and the required energy have to be updated as well. We get:

t' = t (1 + A / )

E' = E (1 + A / )

Thus, both are subject to the same increase. With these formulas, the boss won't have to wonder why his ships are never on time. When the trip takes three days in calm seas, he will expect the eleven hour delay for the above sea conditions. This is no doubt helpful for the work atmosphere.

As stated, the increase in distance is only dictated by the steepness. Hence, higher waves don't necessarily mean more distance. If the amplitude were A = 1 m and the wave length = 8 m, the increase would still be 15 % since the ratio A / didn't change. While this seems odd at first, it makes sense when considering that while the waves are higher in this case, the higher wave length means that we can fit less of them between the two ports.

While focusing on the sine waves, we missed a great optimization problem our boss might have been interested in. Let's look at ship transportation from a monetary point of view. Suppose each trip brings in R0 dollars in revenues. If the ship travels with speed v and the distance between the ports is d, the revenues per unit time are:

dR/dt = R0 / t = R0 v / d

So faster traveling means higher revenues per unit time no surprise there. Note that we did not include the time required to load and unload the ship. We assume it to be small compared to the overall travel time, but if you like, you can include the idletime in your own calculations. What about the costs? The crew is paid C0 per unit time. Then there are also the energy costs. We already found that one trip requires the amount of energy E = k v d. Denoting by e the costs of one unit of energy, we can thus express the costs per unit time as such:

dC/dt = e k v d / t + C0 = e k v3 + C0

So faster traveling also means a lot higher costs this might be a surprise. The profit per unit time is:

dP/dt = dR/dt dC/dt

dP/dt = R v / d e k v C

Is there a speed that would maximize our profits? Indeed there is and it would be a great loss for our company if we overlooked that. So let's find it. To do that, we find the first derivative with respect to v and set it to zero:

R / d 3 e k v = 0

Solving for v we find that:

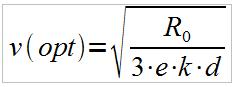
So if the energy costs go up (greater e) or the sea becomes rougher (greater d), we should tell the captain to slow down.

• CarFollowing Models

Suppose a car is traveling on a road at the speed u(t) at time t. Another car approaches this car from behind and starts following it. Obviously the driver of the car that is following cannot choose his speed freely. Rather, his speed v(t) at time t will be a result of whatever the driver in the leading car is doing.