Infosys Science Foundation Series Infosys Science Foundation Series in Mathematical Sciences
Series Editors
Irene Fonseca
Carnegie Mellon University, Pittsburgh, PA, USA
Gopal Prasad
University of Michigan, Ann Arbor, USA
Editorial Board
Manindra Agrawal
Indian Institute of Technology Kanpur, Kanpur, India
Weinan E
Princeton University, Princeton, USA
Chandrashekhar Khare
University of California, Los Angeles, USA
Mahan Mj
Tata Institute of Fundamental Research, Mumbai, India
Ritabrata Munshi
Tata Institute of Fundamental Research, Mumbai, India
S. R. S Varadhan
New York University, New York, USA
The Infosys Science Foundation SeriesThe Infosys Science Foundation Series is a collaborative effort between the Infosys Science Foundation and Springer to publish high quality content. All content published in the Series is written, edited, or vetted by the laureates or jury members of the Infosys Prize. This umbrella series publishes content across academic domains, including, but not limited to, Applied Sciences, Engineering, Pure Sciences, and Mathematics. With this Series, Springer and the Infosys Science Foundation hope to provide readers with textbooks, monographs, handbooks, and professional books of the highest academic quality. Literature in this Series will appeal to a wide audience of researchers, students, educators, and professionals across disciplines.
in Mathematical Sciences, a Scopus-indexed book series, is a sub-series of the Infosys Science Foundation Series. This sub-series focuses on high-quality content in the domain of mathematical sciences and various disciplines of mathematics, statistics, bio-mathematics, financial mathematics, applied mathematics, operations research, applied statistics and computer science. All content published in the sub-series are written, edited, or vetted by the laureates or jury members of the Infosys Prize. With this series, Springer and the Infosys Science Foundation hope to provide readers with monographs, handbooks, professional books and textbooks of the highest academic quality on current topics in relevant disciplines. Literature in this sub-series will appeal to a wide audience of researchers, students, educators, and professionals across mathematics, applied mathematics, statistics and computer science disciplines.
More information about this subseries at http://www.springer.com/series/13817
Ramji Lal
Algebra 3
Homological Algebra and Its Applications
1st ed. 2021
Logo of the publisher
Ramji Lal
University of Allahabad, Prayagraj, Uttar Pradesh, India
ISSN 2363-6149 e-ISSN 2363-6157
Infosys Science Foundation Series
ISSN 2364-4036 e-ISSN 2364-4044
Infosys Science Foundation Series in Mathematical Sciences
ISBN 978-981-33-6325-0 e-ISBN 978-981-33-6326-7
https://doi.org/10.1007/978-981-33-6326-7
Springer Nature Singapore Pte Ltd. 2021
This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed.
The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use.
The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, expressed or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This Springer imprint is published by the registered company Springer Nature Singapore Pte Ltd.
The registered company address is: 152 Beach Road, #21-01/04 Gateway East, Singapore 189721, Singapore
Dedicated to the memory of
my father like brother
(Late) Sri Gopal Lal
Preface
Algebra has played a central and a decisive role in formulating and solving the problems in all branches of mathematics, science, and engineering. My earlier plan was to write a series of three volumes on algebra covering a wide spectrum to cater the need of students and researchers at various levels. The two initial volumes have already appeared. However, looking at the size and the contents to be covered, we decided to split the third volume into two volumes, Algebra 3 and Algebra 4. Algebra 3 concentrates on the homological algebra together with its important applications in mathematics, whereas Algebra 4 is about Lie algebras, Chevalley groups, and their representation theory.
Homological algebra has played and is playing a pivotal role in understanding and classifying (up to certain equivalences) the mathematical structures such as topological, geometrical, arithmetical, and the algebraic structures by associating computable algebraic invariants to these structures. Indeed, it has also shown its deep intrinsic presence in dealing with the problems in physics, in particular, in string theory and quantum theory. The present volume, Algebra 3, the third volume in the series, is devoted to introduce the homological methods and to have some of its important applications in geometry, topology, algebraic geometry, algebra, and representation theory. It contains category theory, abelian categories, and homology theory in abelian categories, the 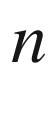 -fold extension functors
-fold extension functors 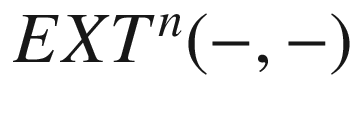 , the torsion functors
, the torsion functors 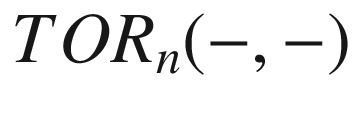 , the theory of derived functors, simplicial and singular homology theories with their applications, co-homology of groups, sheaf theory, sheaf co-homology, some amount of algebraic geometry,
, the theory of derived functors, simplicial and singular homology theories with their applications, co-homology of groups, sheaf theory, sheaf co-homology, some amount of algebraic geometry, 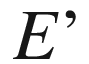 tale sheaf theory and co-homology, and the
tale sheaf theory and co-homology, and the  -adic co-homology with a demonstration showing its application in the representation theory. The book can act as a text for graduate and advance graduate students specializing in mathematics.
-adic co-homology with a demonstration showing its application in the representation theory. The book can act as a text for graduate and advance graduate students specializing in mathematics.















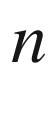 -fold extension functors
-fold extension functors 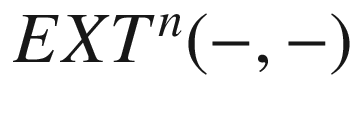 , the torsion functors
, the torsion functors 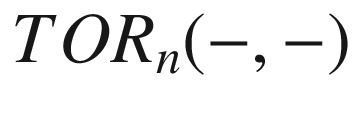 , the theory of derived functors, simplicial and singular homology theories with their applications, co-homology of groups, sheaf theory, sheaf co-homology, some amount of algebraic geometry,
, the theory of derived functors, simplicial and singular homology theories with their applications, co-homology of groups, sheaf theory, sheaf co-homology, some amount of algebraic geometry, 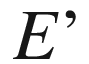 tale sheaf theory and co-homology, and the
tale sheaf theory and co-homology, and the  -adic co-homology with a demonstration showing its application in the representation theory. The book can act as a text for graduate and advance graduate students specializing in mathematics.
-adic co-homology with a demonstration showing its application in the representation theory. The book can act as a text for graduate and advance graduate students specializing in mathematics.