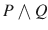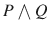The principal aim of this small and brief chapter is to provide a logical foundation to sound mathematical reasoning, and also to understand adequately the notion of a mathematical proof. Indeed, the incidence of paradoxes (Russells and Cantors paradoxes) during the turn of the 19th century led to a strong desire among mathematicians to have a rigorous foundation to all disciplines in mathematics. In logic, the interest is in the form rather than the content of the statements.
1.1 Statements, Propositional Connectives
In mathematics, we are concerned about the truth or the falsity of the statements involving mathematical objects. Yet, one need not take the trouble to define a statement. It is a primitive notion which everyone inherits. Following are some examples of statements.
Man is the most intelligent creature on the earth.
Charu is a brave girl, and Garima is an honest girl.
Sun rises from the east or sun rises from the west.
Shipra will not go to school.
If Gaurav works hard, then he will pass.
Gunjan can be honest if and only if she is brave.
Kishore has a wife implies he is married.
Indira Gandhi died martyr implies and implied by she was brave.
For every river, there is an origin.
There exists a man who is immortal.
The sentences Who is the present President of India?, When did you come?, and Bring me a glass of water are not statements. A statement asserts something(true or false).
We have some operations on the class of statements, namely and, or, If ..., then ..., if and only if (briefly iff), implies, and not. In fact, we consider a suitable class of statements (called the valid statements) which is closed under the above operations. These operations are called the propositional connectives .
The rules which govern the formation of valid statements are in very much use (like those of english grammar) without being conscious of the fact, and it forms the content of the propositional calculus . For the formal development of the language, one is referred to an excellent book entitled Set Theory and Continuum Hypothesis by P.J. Cohen. Here, in this text, we shall adopt rather the traditional informal language.
Conjunction
The propositional connective and is used to conjoin two statements. The conjunction of a statement P and a statement Q is written as P and Q . The symbol
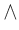
is also used for and . Thus,
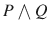
also denotes the conjunction of P and Q . The example 2 above is an example of a conjunction.
Disjunction
The propositional connective or is used to obtain the disjunction of two statements. The disjunction of a statement P and a statement Q is written as P or Q . The symbol
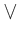
is also used for or . The disjunction of a statement P and a statement Q is also written as
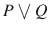
. The example 3 above is an example of a disjunction.
Negation
Usually not is used at a suitable place in a statement to obtain the negation of the statement. The negation of a statement P is denoted by - P . The example 4 above is the negation of Shipra will go to school. The negation of this statement can also be expressed by -(Shipra will go to school).
Conditional statement
A statement of the form
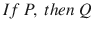
is called a
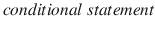
. The statement P is called the antecedent or the hypothesis , and Q is called the consequent or the conclusion . The example 5 above is a conditional statement. If P , then Q is also expressed by saying that Q is a necessary condition for P . An other way to express it is to say that P is a sufficient condition for Q .
Implication
A statement of the form P implies Q (in symbol
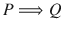
) is called an implication . The statement
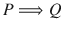
and the statement If P , then Q are logically same, for (as we shall see) the truth values of both the statements are always same. Again, P is called the antecedent or the hypothesis , and Q is called the consequent or the conclusion . Example 7 is an implication .
Equivalence
A statement of the form P if and only if Q (briefly
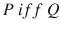
) is called an equivalence . P implies and implied by Q (in symbol

) is logically same as P if and only if Q . We also express it by saying that P is a necessary and sufficient condition for Q . Examples 6 and 7 are equivalences.
1.2 Statement Formula and Truth Functional Rules
A statement variable is a variable which can take any value from the class of valid atomic statements (statements without propositional connectives). We use the notations
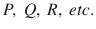
for the statement variables. A well-formed statement formula is a finite string of the statement variables, the propositional connectives, and the parenthesis limiting the scopes of connectives. Thus, for example,
and
are well-formed statement formulas.
The rules of dependence of the truth value of a statement formula on the truth values of its statement variables (atomic parts) (which are prompted by our common sense) are called the
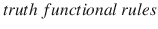
. These rules are illustrated by tables called the
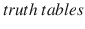
.
The truth functional rule for the conjunction
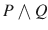
The statement formula
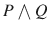













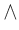 is also used for and . Thus,
is also used for and . Thus, 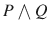 also denotes the conjunction of P and Q . The example 2 above is an example of a conjunction.
also denotes the conjunction of P and Q . The example 2 above is an example of a conjunction.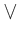 is also used for or . The disjunction of a statement P and a statement Q is also written as
is also used for or . The disjunction of a statement P and a statement Q is also written as 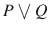 . The example 3 above is an example of a disjunction.
. The example 3 above is an example of a disjunction.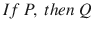 is called a
is called a 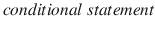 . The statement P is called the antecedent or the hypothesis , and Q is called the consequent or the conclusion . The example 5 above is a conditional statement. If P , then Q is also expressed by saying that Q is a necessary condition for P . An other way to express it is to say that P is a sufficient condition for Q .
. The statement P is called the antecedent or the hypothesis , and Q is called the consequent or the conclusion . The example 5 above is a conditional statement. If P , then Q is also expressed by saying that Q is a necessary condition for P . An other way to express it is to say that P is a sufficient condition for Q .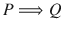 ) is called an implication . The statement
) is called an implication . The statement 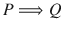 and the statement If P , then Q are logically same, for (as we shall see) the truth values of both the statements are always same. Again, P is called the antecedent or the hypothesis , and Q is called the consequent or the conclusion . Example 7 is an implication .
and the statement If P , then Q are logically same, for (as we shall see) the truth values of both the statements are always same. Again, P is called the antecedent or the hypothesis , and Q is called the consequent or the conclusion . Example 7 is an implication .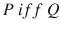 ) is called an equivalence . P implies and implied by Q (in symbol
) is called an equivalence . P implies and implied by Q (in symbol  ) is logically same as P if and only if Q . We also express it by saying that P is a necessary and sufficient condition for Q . Examples 6 and 7 are equivalences.
) is logically same as P if and only if Q . We also express it by saying that P is a necessary and sufficient condition for Q . Examples 6 and 7 are equivalences.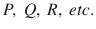 for the statement variables. A well-formed statement formula is a finite string of the statement variables, the propositional connectives, and the parenthesis limiting the scopes of connectives. Thus, for example,
for the statement variables. A well-formed statement formula is a finite string of the statement variables, the propositional connectives, and the parenthesis limiting the scopes of connectives. Thus, for example, 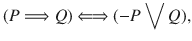
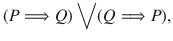
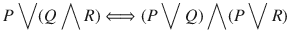
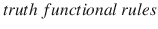 . These rules are illustrated by tables called the
. These rules are illustrated by tables called the 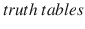 .
.