Massimiliano Bonamente - Statistics and Analysis of Scientific Data
Here you can read online Massimiliano Bonamente - Statistics and Analysis of Scientific Data full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 0, publisher: Springer New York, New York, NY, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Statistics and Analysis of Scientific Data
- Author:
- Publisher:Springer New York, New York, NY
- Genre:
- Year:0
- Rating:4 / 5
- Favourites:Add to favourites
- Your mark:
- 80
- 1
- 2
- 3
- 4
- 5
Statistics and Analysis of Scientific Data: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Statistics and Analysis of Scientific Data" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Statistics and Analysis of Scientific Data — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Statistics and Analysis of Scientific Data" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
- The complementary
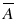 of an event A is the set of all possible outcomes except those in A . For example, the complementary of the event odd number is the event even number.
of an event A is the set of all possible outcomes except those in A . For example, the complementary of the event odd number is the event even number. - Given two events A and B , the union C = A B is the event comprising all outcomes of A and those of B . In the roll of a die, the union of odd and even numbers is the sample space itself, consisting of all possible outcomes.
- The intersection of two events C = A B is the event comprising all outcomes of A that are also outcomes of B . When A B =, the events are said to be mutually exclusive . The union and intersection can be naturally extended to more than two events.
- A number of events A i are said to be a partition of the sample space if they are mutually exclusive, and if their union is the sample space itself, A i =.
- When all outcomes in A are comprised in B , we will say that A B or B A .
- The probability of an event A is a non-negative number, P ( A )0;
- The probability of all possible outcomes, or sample space, is normalized to the value of unity, P ()=1;
- If A and B are mutually exclusive events, thenFigure illustrates this property using set diagrams. For events that are not mutually exclusive, this property does not apply. The probability of the union is represented by the area of A B , and the outcomes that overlap both events are not double-counted.
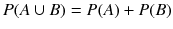 (1.1)
(1.1)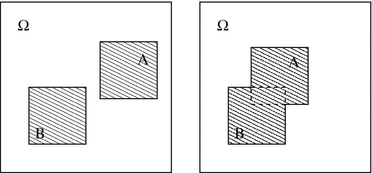 Fig. 1.1The probability of the event P ( A B ) is the sum of the two individual probabilities, only if the two events are mutually exclusive. This property enables the interpretation of probability as the area of a given event within the sample space
Fig. 1.1The probability of the event P ( A B ) is the sum of the two individual probabilities, only if the two events are mutually exclusive. This property enables the interpretation of probability as the area of a given event within the sample space
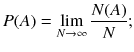
Font size:
Interval:
Bookmark:
Similar books «Statistics and Analysis of Scientific Data»
Look at similar books to Statistics and Analysis of Scientific Data. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Statistics and Analysis of Scientific Data and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.












