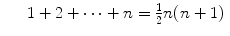The underlying space for all the analysis in this book is the set of real numbers. In this chapter we set down some basic properties of this set. These properties will serve as our axioms in the sense that it is possible to derive all the properties of the real numbers using only these axioms. However, we will avoid getting bogged down in this endeavor. Some readers may wish to refer to the appendix on set notation.
1 The Set
of Natural Numbers
We denote the set {1,2,3,} of all positive integers by
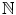
. Each positive integer n has a successor, namely n +1. Thus the successor of 2 is 3, and 37 is the successor of 36. You will probably agree that the following properties of
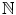
are obvious; at least the first four are.
N1.
1 belongs to
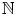
.
N2.
If n belongs to
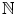
, then its successor n +1 belongs to
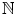
.
N3.
1 is not the successor of any element in
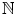
.
N4.
If n and m in
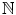
have the same successor, then n = m .
N5.
A subset of
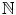
which contains 1, and which contains n +1 whenever it contains n , must equal
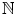
.
Properties N1 through N5 are known as the Peano Axioms or Peano Postulates . It turns out most familiar properties of
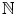
can be proved based on these five axioms; see [].
Lets focus our attention on axiom N5, the one axiom that may not be obvious. Here is what the axiom is saying. Consider a subset S of
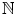
as described in N5. Then 1 belongs to S . Since S contains n +1 whenever it contains n , it follows that S contains
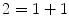
. Again, since S contains n +1 whenever it contains n , it follows that S contains
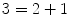
. Once again, since S contains n +1 whenever it contains n , it follows that S contains
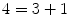
. We could continue this monotonous line of reasoning to conclude S contains any number in
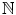
. Thus it seems reasonable to conclude
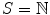
. It is this reasonable conclusion that is asserted by axiom N5.
Here is another way to view axiom N5. Assume axiom N5 is false. Then
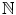
contains a set S such that
(ii)
If n S , then n +1 S ,
and yet
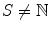
. Consider the smallest member of the set
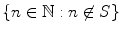
, call it n 0. Since (i) holds, it is clear n 01. So n 0 is a successor to some number in
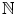
, namely n 01. We have n 01 S since n 0 is the smallest member of
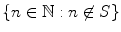
. By (ii), the successor of n 01, namely n 0, is also in S , which is a contradiction. This discussion may be plausible, but we emphasize that we have not proved axiom N5 using the successor notion and axioms N1 through N4, because we implicitly used two unproven facts. We assumed every nonempty subset of
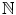
contains a least element and we assumed that if n 01 then n 0 is the successor to some number in
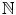
.
Axiom N5 is the basis of mathematical induction. Let
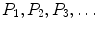
be a list of statements or propositions that may or may not be true. The principle of mathematical induction asserts all the statements
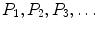
are true provided
(I1 ) P 1 is true,
(I2 ) P n +1 is true whenever P n is true.
We will refer to (I1), i.e., the fact that P 1 is true, as the basis for induction and we will refer to (I2) as the induction step. For a sound proof based on mathematical induction, properties (I1) and (I2) must both be verified. In practice, (I1) will be easy to check.
Example 1
Prove
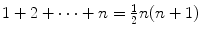
for positive integers n .
Solution
Our n th proposition is
Thus P 1 asserts
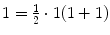
, P 2 asserts
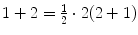
, P 37 asserts
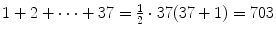
, etc. In particular, P 1 is a true assertion which serves as our basis for induction.
For the induction step, suppose P n is true. That is, we suppose














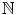 of Natural Numbers
of Natural Numbers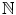 . Each positive integer n has a successor, namely n +1. Thus the successor of 2 is 3, and 37 is the successor of 36. You will probably agree that the following properties of
. Each positive integer n has a successor, namely n +1. Thus the successor of 2 is 3, and 37 is the successor of 36. You will probably agree that the following properties of 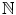 are obvious; at least the first four are.
are obvious; at least the first four are. 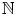 .
.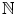 , then its successor n +1 belongs to
, then its successor n +1 belongs to 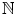 .
.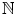 .
.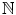 have the same successor, then n = m .
have the same successor, then n = m .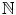 which contains 1, and which contains n +1 whenever it contains n , must equal
which contains 1, and which contains n +1 whenever it contains n , must equal 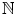 .
.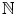 can be proved based on these five axioms; see [].
can be proved based on these five axioms; see [].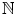 as described in N5. Then 1 belongs to S . Since S contains n +1 whenever it contains n , it follows that S contains
as described in N5. Then 1 belongs to S . Since S contains n +1 whenever it contains n , it follows that S contains 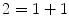 . Again, since S contains n +1 whenever it contains n , it follows that S contains
. Again, since S contains n +1 whenever it contains n , it follows that S contains 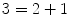 . Once again, since S contains n +1 whenever it contains n , it follows that S contains
. Once again, since S contains n +1 whenever it contains n , it follows that S contains 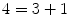 . We could continue this monotonous line of reasoning to conclude S contains any number in
. We could continue this monotonous line of reasoning to conclude S contains any number in 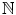 . Thus it seems reasonable to conclude
. Thus it seems reasonable to conclude 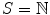 . It is this reasonable conclusion that is asserted by axiom N5.
. It is this reasonable conclusion that is asserted by axiom N5.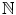 contains a set S such that
contains a set S such that 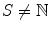 . Consider the smallest member of the set
. Consider the smallest member of the set 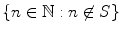 , call it n 0. Since (i) holds, it is clear n 01. So n 0 is a successor to some number in
, call it n 0. Since (i) holds, it is clear n 01. So n 0 is a successor to some number in 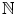 , namely n 01. We have n 01 S since n 0 is the smallest member of
, namely n 01. We have n 01 S since n 0 is the smallest member of 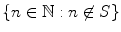 . By (ii), the successor of n 01, namely n 0, is also in S , which is a contradiction. This discussion may be plausible, but we emphasize that we have not proved axiom N5 using the successor notion and axioms N1 through N4, because we implicitly used two unproven facts. We assumed every nonempty subset of
. By (ii), the successor of n 01, namely n 0, is also in S , which is a contradiction. This discussion may be plausible, but we emphasize that we have not proved axiom N5 using the successor notion and axioms N1 through N4, because we implicitly used two unproven facts. We assumed every nonempty subset of 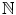 contains a least element and we assumed that if n 01 then n 0 is the successor to some number in
contains a least element and we assumed that if n 01 then n 0 is the successor to some number in 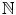 .
.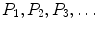 be a list of statements or propositions that may or may not be true. The principle of mathematical induction asserts all the statements
be a list of statements or propositions that may or may not be true. The principle of mathematical induction asserts all the statements 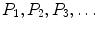 are true provided
are true provided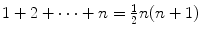 for positive integers n .
for positive integers n .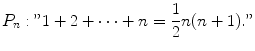
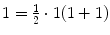 , P 2 asserts
, P 2 asserts 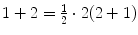 , P 37 asserts
, P 37 asserts 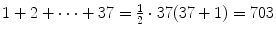 , etc. In particular, P 1 is a true assertion which serves as our basis for induction.
, etc. In particular, P 1 is a true assertion which serves as our basis for induction.