Haynes - GCSE Maths Notes

GCSE MATHS NOTES
A Haynes MSc, Copyright 2005-2018

---

INTRODUCTION
My GCSE Maths Notes:

• Are self-contained i.e. do not assume prior knowledge of the subject (they are not simply brief revision notes)
• Are somewhat longer than the notes I've provided students with in class, but (deliberately) not as long as typical equivalent textbooks
  • They are about 200 sides of A4 if printed out in the webpage format that I wrote them
• Cover the subject content of a UK syllabus I've taught a number of times
  • Your syllabus may be different, but a lot of the material will probably still be relevant

The contents of the GCSE Maths Notes is summarised below:
(For clickable links, view ):

• Part 1: NUMBER - Numbers, Money - Chapters 1 - 6
• Part 2: ALGEBRA - Algebraic expressions & relationships, Graphs - Chapters 7 - 12
• Part 3: SHAPE, SPACE AND MEASURES - Chapters 13 -20
• Part 4: HANDLING DATA - Statistics, Probability - Chapters 21 - 24

Note - if you're not familiar with UK qualifications - GCSEs are typically aimed at 14-16 year olds

---

Note - Some ebook (kindles etc.) readers (including phones) auto-shrink some items on screen:

• If something looks very small on your device (an image , an equation or text ) - you may be able to:
  • Enlarge it by (double) clicking it - and (double) click it again to shrink it

---

GCSE Maths Notes
Copyright 2005-2018 A Haynes

GCSE MATHS NOTES
A Haynes MSc, Copyright 2005-2018

---

TABLE OF CONTENTS
Part 1: NUMBER
Numbers

• - Types Of Numbers; Directed Numbers;
  The Decimal System
• - Number Patterns; Factors And Multiples; Fractions
• - Percentages; Indices; Roots
• - Standard Form; Approximations;
  Proportional Division; Direct And Inverse Proportion

Money

• - Pay; Tax; Household Expenses
• - Credit; Savings - Compound Interest; Travel

Part 2: ALGEBRA
Algebraic expressions & relationships

• - Using Symbols; Simplifying Algebraic Expressions;
  Factorising Algebraic Expressions
• - Algebraic Fractions; Equations;
  Simultaneous Equations; Formulae
• - Quadratic Equations; Finding A Solution
  By Trial And Improvement; Inequalities; Flow Charts

Graphs

• - Cartesian Coordinates; Straight Line Graphs;
  Parabolas; Cubic Functions; Rectangular Hyperbola; Exponential Functions
• - Solving Equations Using Graphs; Equations
  Changed To Linear Graphical Form; Transformation Of Functions/Graphs;
  Graphs And Inequalities
• - Travel Graphs

Part 3: SHAPE, SPACE AND MEASURES
Shape

• - Angles And Lines; Polygons
• - Congruence And Similarity; Symmetry; Circles;
  Geometrical Constructions
• - Trigonometry

Space

• - Bearings; Angles Of Elevation And Depression;
  Scales; Loci; Tessellations
• - Vectors
• - Transformations

Measures

• - Units; Areas Of Plane Surfaces; Volumes Of Cubes
  And Cuboids
• - Areas And Volumes Of Various 3D Objects;
  Dimensions And Formulae

Part 4: HANDLING DATA
Statistics

• - Terminology; Representing Data Visually;
  Statistical Surveys
• - Averages; Dispersion Of Data
• - Frequency Distributions;
  Grouped Frequency Distributions

Probability

• - Basic Ideas; Range Of Probabilities;
  Total Probability; Mutually Exclusive Events - The Addition Law;
  Independent Events - The Multiplication Law; Probability Tree;
  Experimental Probability; Conditional Probability

---

GCSE Maths Notes
Copyright 2005-2018 A Haynes

Numbers (Chapters 1 to 4)

---

Chapter 1

• 
  
• Please Note - If an image , an equation or text appears very small on your device - you may be able to:
  • Enlarge it by (double) clicking it - and (double) click it again to shrink it

---

TYPES OF NUMBERS -

Numbers fall into certain groups, some of which are given names:

• Counting numbers : 1, 2, 3, 4, ...............
• Natural numbers : 0, 1, 2, 3, 4, ..............
• Integers : .........., -4, -3, -2, -1, 0, 1, 2, 3, 4, .........

The above series of numbers all continue indefinitely.

• Rational numbers are those which can be expressed as fractions, i.e. one number divided by another

Since dividing any number by 1 leaves the number unchanged, all the above numbers are rational numbers because we could express each one as, for example:

• 1/1, 2/1, 3/1 etc.

The following are also rational numbers:

Some numbers cannot be expressed as exact fractions. For example, we say that the square root of 9 is 3, because 3x 3=9. But what about the square root of, for example, 2? On the calculator you will get something like:

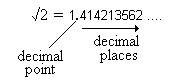
The decimal places carry on forever without repeating, which means that the number cannot be expressed as a fraction, i.e. it is not a rational number. Hence, we describe the square root of 2 is an irrational number .

• Rational and irrational numbers together form what are called real numbers

Any real number, rational or irrational, can be located on the real number line - this is represented below - it extends forever to right and left: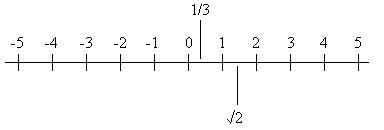Changing a recurring decimal into a fraction

This is illustrated with a couple of examples:

Example

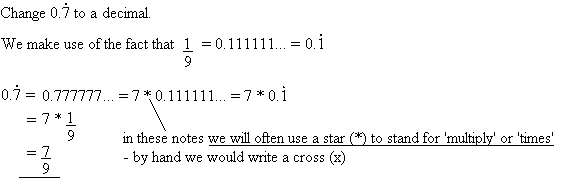
Example

Arithmetic

Arithmetic is the branch of maths concerned with numerical calculations.

There are four basic operations with numbers :

• Addition , which produces the sum of two numbers:

The sum of 2 and 5 equals 7, which we write as: 2 + 5 = 7

• Subtraction , which produces the difference between two numbers:

The difference between 9 and 5 is 4, which we write as: 9 - 5 = 4

• Multiplication , which produces the product of two numbers:

The product of 3 and 4 is 12, which we write as: 3 * 4 = 12

[Again note that we here use the star (*) to stand for 'times' or 'multiply by' - whereas by hand we would usually write a cross (x )]

• Division , which produces the quotient of two numbers:

---

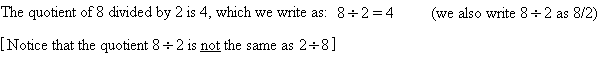
DIRECTED NUMBERS -

Directed numbers are positive or negative numbers. When you add, subtract, multiply or divide directed numbers, you are moving from one point to another along the number line:

Next page